

|
SHORTEST HALF MIDMEANName:
\( m = n/2 \hspace{1.35in} n \mbox{ odd} \)
where <y> is the response variable; <par> is a parameter where the computed shortest half midmean is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; <par> is a parameter where the computed difference of shortest half midmeans is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET A = SHORTEST HALF MIDMEAN Y1 SUBSET TAG > 2 LET A = DIFFERENCE OF SHORTEST HALFMIDMEAN Y1 Y2
Andrews, Bickel, Hampel, Huber, Rogers, and Tukey (1972), "Robust Estimates of Location", Princeton University Press, Princeton. Rousseeuw (1985), "Multivariate Estimation with High Breakdown Point", in Grossman, Pflug, Nincze, Wetrz (eds), "Mathematical Statistics and Applications", Reidel, Dordrecht, The Netherlands, pp. 283-297.
2017/06: Added DIFFERENCE OF SHORTEST HALF MIDMEAN
SKIP 25
READ LGN.DAT Y
LET SHMM = SHORTEST HALF MIDMEAN Y
Program 2:
. Step 1: Create the data
.
skip 25
read gear.dat y x
skip 0
.
char X
line blank
y1label Shortest Half Midmean
x1label Group
x1tic mark offset 0.5 0.5
label case asis
title case asis
title Shortest Half Midmean of GEAR.DAT
title offset 2
.
set statistic plot reference line average
shortest half midmean plot y x
.
set write decimals 5
tabulate shortest half midmean y x
The following output is generated
SKIP 25 READ IRIS.DAT Y1 TO Y4 X . LET A = DIFFERENCE OF SHORTEST HALF MIDMEAN Y1 Y2 SET WRITE DECIMALS 4 TABULATE DIFFERENCE OF SHORTEST HALF MIDMEAN Y1 Y2 X 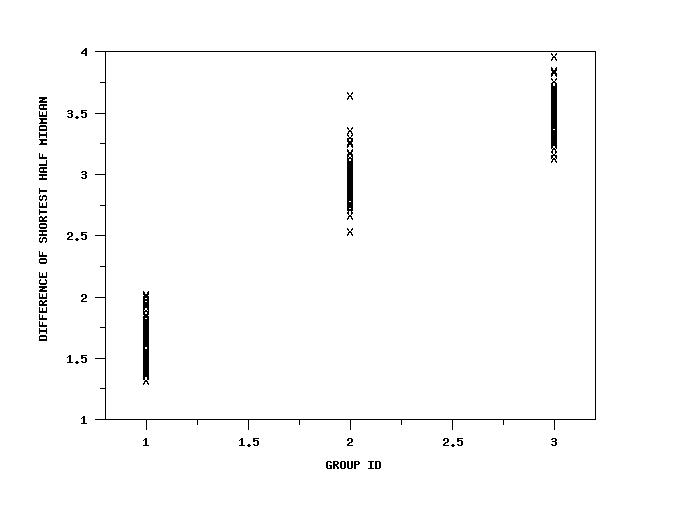
|
Privacy
Policy/Security Notice
NIST is an agency of the U.S.
Commerce Department.
Date created: 07/03/2017 | |||||||||||||||||||