SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

YULPPF

Name:
    YULPPF (LET)
Type:
    Library Function
Purpose:
    Compute the Yule percent point function.
Description:
    The Yule distribution has the following probability mass function:

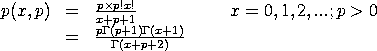
      p(x,p) = p*p!*x!/(x+p+1)! p > 0, x = 0, 1, 2, ... = p*GAMMA(p+1)*GAMMA(x+1)/GAMMA(x+p+2)

    with p denoting the shape parameter and GAMMA denoting the gamma function (HELP GAMMA for details).

    Dataplot computes the Yule probability density function using the log gamma function. The Yule distribution has increasingly long tails as p goes to zero. Currently, Dataplot limits the Yule ppf function to the case where p >= 0.1.

    The cumulative distribution function is the sum from 0 to x. The percent point function is the inverse of the cumulative distribution function. That is, given the probability, the appropriate value of x is returned. The percent point is determined by computing the terms of the Yule cdf function until the requested probability value is obtained.

Syntax:
    LET <y> = YULPPF(<x>,<p>)             <SUBSET/EXCEPT/FOR qualification>
    where <x> is a non-negative integer number, parameter, or variable in the interval (0,1);
                <p> is a positive number, parameter, or variable that specifies the shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed Yule ppf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = YULPPF(0.95,1.5)
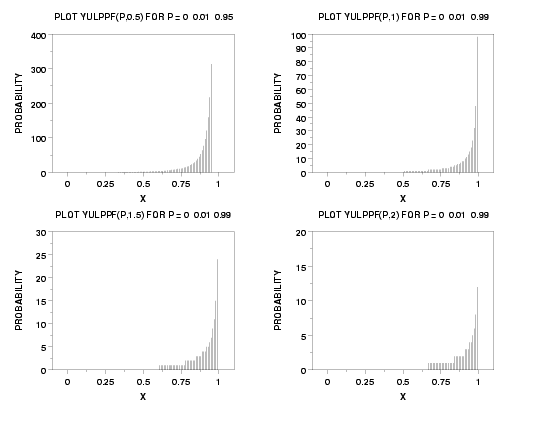
    LET A = YULPPF(X,P)
    PLOT YULPPF(X,2) FOR X = 0 0.01 0.95
Note:
    The Yule is a special case of the Waring distribution. Specifically,

      YULPPF(X,P) = WARPPF(X,P-1,1)
Default:
    None
Synonyms:
    None
Related Commands:
    YULCDF = Compute the Yule cumulative distribution function.
    YULPPF = Compute the Yule percent point function.
    WARPDF = Compute the Waring probability density function.
    BBNPDF = Compute the beta-binomial probability density function.
    GEOPDF = Compute the geometric probability density function.
    NBPDF = Compute the negative binomial probability density function.
    HYPPDF = Compute the hypergeometric probability density function.
Reference:
    "Discrete Univariate Distributions", Second Edition, Johnson, Kotz, and Kemp, John Wiley & Sons, 1994 (pp. 274-279).
Applications:
    Distributional Modeling
Implementation Date:
    2004/4
Program: 
     
X1LABEL Probability
Y1LABEL X
LABEL CASE ASIS
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
XTIC OFFSET 0.1 0.1
LINE BLANK
SPIKE ON
TITLE AUTOMATIC
X1LABEL X
Y1LABEL PROBABILITY
TITLE SIZE 3
PLOT YULPPF(P,0.5) FOR P = 0  0.01  0.95
PLOT YULPPF(P,1) FOR P = 0  0.01  0.99
PLOT YULPPF(P,1.5) FOR P = 0  0.01 0.99
PLOT YULPPF(P,2) FOR P = 0  0.01  0.99
END OF MULTIPLOT
    plot generated by sample program

Date created: 7/7/2004
Last updated: 7/7/2004
Please email comments on this WWW page to [email protected].