







We have included both generated and "real-world" nonlinear least squares problems of varying levels of difficulty. The generated datasets are designed to challenge specific computations. Real-world data include challenging datasets such as the Thurber problem, and more benign datasets such as Misra1a. The certified values are "best-available" solutions, obtained using 128-bit precision and confirmed by at least two different algorithms and software packages using analytic derivatives.
Users might also want to test their nonlinear least squares procedures on the linear least squares problems provided at this Web site. For some of these test problems, however, it is unreasonable to expect the correct solution from a nonlinear least squares procedure when finite difference derivatives are used. Many of these problems (for example, the Longley and Wampler datasets) are troublesome to solve even for the best codes. These difficult problems are impossible to solve correctly when the matrix of predictor variables is only approximate because the user did not supply analytic derivatives.
As noted in the General Background Information, the datasets have been ordered by level of difficulty (lower, average, and higher). This ordering is meant to provide rough guidance for the user. Producing correct results on all datasets of higher difficulty does not imply that your software will correctly solve all datasets of average or even lower difficulty. Similarly, producing correct results for all datasets in this collection does not imply that your software will do the same for your own particular dataset. It will, however, provide some degree of assurance, in the sense that your package provides correct results for datasets known to yield incorrect results for some software.
The robustness and reliability of nonlinear least squares software depends on the algorithm used and how it is implemented, as well as on the characteristics of the actual problem being solved. Nonlinear least squares solvers are particularly sensitive to the starting values provided for a given problem. For this reason, we provide three sets of starting values for each problem: the first is relatively far from the final solution; the second relatively close; and the third is the actual certified solution. For example, Figure 1 shows a sum of squares contour plot for dataset BoxBOD. The existence of the local minimum (shown as the blue contour in the lower left corner of the plot) makes this problem especially difficult from the "far" starting value.
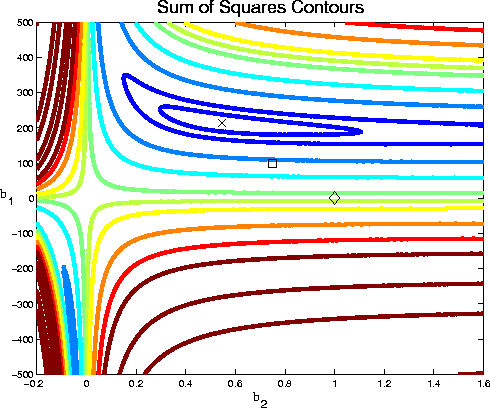 | |
|---|---|
| |
| Figure 1: Starting Values for Dataset BoxBOD |
We recognize that a practitioner will choose starting values carefully, and will attempt to provide starting values as close to the expected solution as possible. We also recognize that sometimes good starting values are not available. For testing purposes, therefore, it is of interest to see how a code will perform when the starting values are not close to the solution, even though such starting values might be ridiculously bad from a practical standpoint. In general, it can be expected that a particular code will fail more often from the starting values far from the solution than from the starting values that are relatively close. How serious it is that a code fails when using starting values far from the solution will depend on the types of problems for which the code will be employed.
It is interesting to see how a solver responds when the certified values are used as starting values. While it would seem that such a test would be trivial for any code, this is frequently not the case. Sometimes codes cannot recognize that they are at a sum of squares minimizer, and so return a warning. This is not an unreasonable outcome. However, we have also seen instances where codes, given the certified values as starting values, return parameter estimates that produce a final residual sum of squares that is significantly larger than the residual sum of squares at the starting (certified) values. Obviously, such results should lead one to question the reliability of the solver.
The certified results are reported to 11 decimal places for each dataset. Clearly, most of these digits are not statistically significant, and we are not advocating that results should be reported to this number of digits in a statistical context. We do believe, however, that this number of digits can be useful when testing the numerical properties of a procedure.
Except in cases where the certified value is essentially zero (for example, as occurs for the three Lanczos problems), a good nonlinear least squares procedure should be able to duplicate the certified results to at least 4 or 5 digits. That is, it should be the case that
There can be several reasons that a given code might not agree with the certified values. First, the code might have found a different local minimum such as is shown in the lower left corner of Figure 1. Since nonlinear least squares procedures are not guaranteed to find the global minimum of the sum of squares, it should not be considered a failure for the tested code to find a different local minimum. However, the existence of the alternate minimum should be tested by restarting the code with starting values selected as close as possible to the new "solution" to see if the procedure will again stop at the same point. If it does, then it can be assumed that a local minimum was found. If not, then it may be that the procedure encountered some numerical difficulty in finding the solution, and that the procedure may not be robust enough to solve the problem in question.
Another reason that a nonlinear least squares procedure might fail is that critical portions of the computations were not done with adequate precision. In general, most of the computations in a nonlinear least squares procedure should be done in double precision on a 32-bit machine, especially if analytic derivatives are not provided by the user. Many of the problems provided in this test suite will severely stress a nonlinear least squares procedure that is written using only single precision arithmetic. Some of these problems are also especially difficult to solve to more than 2 or 3 digits of accuracy when finite difference derivatives are used, even for codes implemented using 64-bit precision.
It is also possible that the algorithm implemented is simply not adequate to handle more computationally challenging problems. While it should not be the case that "ease of use" has to be traded for robustness and reliability, it often appears to be that this is so. When this happens, users must determine how well the procedure works on the class of problems they intend to solve.
Finally, as mentioned above, it is important to note what a procedure does when it fails to find the solution. Does it provide the user with some indication that there might be problems with the results provided, or does it give questionable results without adequate warning. In general, an incorrect result supplied without warning is more troublesome than a correct result identified as questionable.
We plan to update this collection of datasets in the future, and welcome your feedback on specific datasets to include, and on other ways to improve this web service.
