1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.1. Autocorrelation Plot
1.3.3.1.2. |
Autocorrelation Plot: Moderate Autocorrelation |
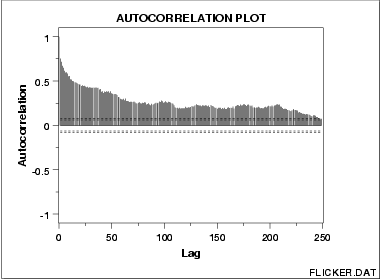
- The data come from an underlying autoregressive model with moderate positive autocorrelation.
-
\[ Y_{i} = A_0 + A_1*Y_{i-1} + E_{i} \]
The randomness assumption for least squares fitting applies to the residuals of the model. That is, even though the original data exhibit non-randomness, the residuals after fitting Yi against Yi-1 should result in random residuals. Assessing whether or not the proposed model in fact sufficiently removed the randomness is discussed in detail in the Process Modeling chapter.
The residual standard deviation for this autoregressive model will be much smaller than the residual standard deviation for the default model
-
\[ Y_{i} = A_0 + E_{i} \]

