1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.27. |
Spectral Plot |
Examine Cyclic Structure
The frequency is measured in cycles per unit time where unit time is defined to be the distance between 2 points. A frequency of 0 corresponds to an infinite cycle while a frequency of 0.5 corresponds to a cycle of 2 data points. Equi-spaced time series are inherently limited to detecting frequencies between 0 and 0.5.
Trends should typically be removed from the time series before applying the spectral plot. Trends can be detected from a run sequence plot. Trends are typically removed by differencing the series or by fitting a straight line (or some other polynomial curve) and applying the spectral analysis to the residuals.
Spectral plots are often used to find a starting value for the frequency, ω, in the sinusoidal model
-
\[ Y_{i} = C + \alpha\sin{(2\pi\omega t_{i} + \phi)} + E_{i} \]
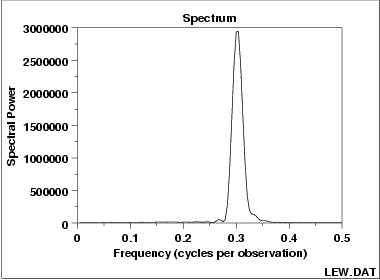
This spectral plot of the LEW.DAT data set shows one dominant frequency of approximately 0.3 cycles per observation.
Variance Versus Frequency
- Vertical axis: Smoothed variance (power)
- Horizontal axis: Frequency (cycles per observation)
- How many cyclic components are there?
- Is there a dominant cyclic frequency?
- If there is a dominant cyclic frequency, what is it?
Check Cyclic Behavior of Time Series
Complex Demodulation Amplitude Plot
Complex Demodulation Phase Plot

