1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.6. Probability Distributions
1.3.6.6. Gallery of Distributions

1.3.6.6.2.

Uniform Distribution

Probability Density Function

The general formula for the probability density function of the uniform distribution is

\( f(x) = \frac{1} {B - A} \;\;\;\;\;\;\; \mbox{for} \ A \le x \le B \)

where A is the location parameter and (B - A) is the scale parameter. The case where A = 0 and B = 1 is called the standard uniform distribution. The equation for the standard uniform distribution is

\( f(x) = 1 \;\;\;\;\;\;\; \mbox{for} \ 0 \le x \le 1 \)

Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the standard form of the function.

The following is the plot of the uniform probability density function.

Cumulative Distribution Function

The formula for the cumulative distribution function of the uniform distribution is

\( F(x) = x \;\;\;\;\;\;\; \mbox{for} \ 0 \le x \le 1 \)

The following is the plot of the uniform cumulative distribution function.

Percent Point Function

The formula for the percent point function of the uniform distribution is

\( G(p) = p \;\;\;\;\;\;\; \mbox{for} \ 0 \le p \le 1 \)

The following is the plot of the uniform percent point function.

Hazard Function

The formula for the hazard function of the uniform distribution is

\( h(x) = \frac{1} {1-x} \;\;\;\;\;\;\; \mbox{for} \ 0 \le x < 1 \)

The following is the plot of the uniform hazard function.

Cumulative Hazard Function

The formula for the cumulative hazard function of the uniform distribution is

\( H(x) = -ln{(1-x)} \;\;\;\;\;\;\; \mbox{for} \ 0 \le x < 1 \)

The following is the plot of the uniform cumulative hazard function.

Survival Function

The formula for the uniform survival function is

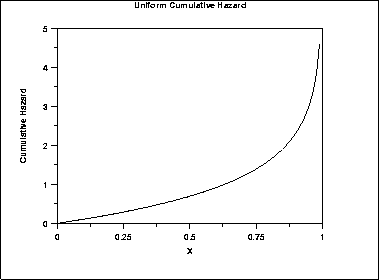
\( S(x) = 1 - x \;\;\;\;\;\;\; \mbox{for} \ 0 \le x \le 1 \)

The following is the plot of the uniform survival function.

Inverse Survival Function

The formula for the uniform inverse survival function is

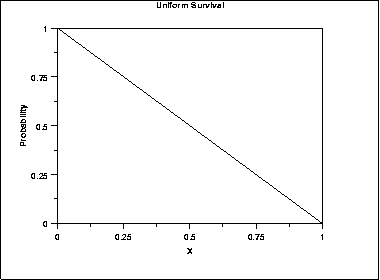
\( Z(p) = 1 - p \;\;\;\;\;\;\; \mbox{for} \ 0 \le p \le 1 \)

The following is the plot of the uniform inverse survival function.

Common Statistics

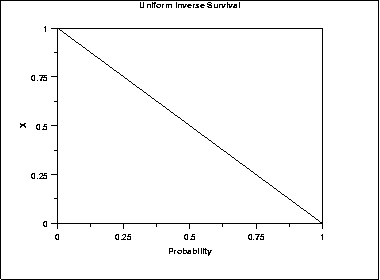
Mean	(A + B)/2
Median	(A + B)/2
Range	B - A
Standard Deviation	\( \sqrt{\frac{(B - A)^{2}} {12}} \)
Coefficient of Variation	\( \frac{(B - A)} {\sqrt{3}(B + A)} \)
Skewness	0
Kurtosis	9/5

Parameter Estimation

The method of moments estimators for A and B are

\( \hat{A} = \bar{x} - \sqrt{3}s \)
\( \hat{B} = \bar{x} + \sqrt{3}s \)

The maximum likelihood estimators are usually given in terms of the parameters a and h where

A = a - h
B = a + h

The maximum likelihood estimators for a and h are

\( \hat{a} = \mbox{midrange}(Y_{1}, Y_{2}, ... , Y_{n}) \)
\( \hat{h} = 0.5[\mbox{range}(Y_{1}, Y_{2}, ... , Y_{n})] \)

This gives the following maximum likelihood estimators for A and B

\( \hat{A} = \mbox{midrange}(Y_{1}, Y_{2}, ... , Y_{n}) - 0.5[\mbox{range}(Y_{1}, Y_{2}, ... , Y_{n})] = Y_{1} \)
\( \hat{B} = \mbox{midrange}(Y_{1}, Y_{2}, ... , Y_{n}) + 0.5[\mbox{range}(Y_{1}, Y_{2}, ... , Y_{n})] = Y_{n} \)

Comments

The uniform distribution defines equal probability over a given range for a continuous distribution. For this reason, it is important as a reference distribution.

One of the most important applications of the uniform distribution is in the generation of random numbers. That is, almost all random number generators generate random numbers on the (0,1) interval. For other distributions, some transformation is applied to the uniform random numbers.

Software

Most general purpose statistical software programs support at least some of the probability functions for the uniform distribution.