1.3. EDA Techniques
1.3.6. Probability Distributions
1.3.6.6. Gallery of Distributions
1.3.6.6.4. |
t Distribution |
\( f(x) = \frac{(1 + \frac{x^2}{\nu})^{\frac{-(\nu + 1)} {2}}} {B(0.5,0.5\nu)\sqrt{\nu}} \)
where B is the beta function and ν is a positive integer shape parameter. The formula for the beta function is
\( B(\alpha,\beta) = \int_{0}^{1} {t^{\alpha-1}(1-t)^{\beta-1}dt} \)
In a testing context, the t distribution is treated as a "standardized distribution" (i.e., no location or scale parameters). However, in a distributional modeling context (as with other probability distributions), the t distribution itself can be transformed with a location parameter, μ, and a scale parameter, σ.
The following is the plot of the t probability density function for 4 different values of the shape parameter.
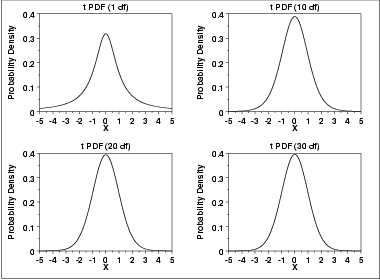
These plots all have a similar shape. The difference is in the heaviness of the tails. In fact, the t distribution with ν equal to 1 is a Cauchy distribution. The t distribution approaches a normal distribution as ν becomes large. The approximation is quite good for values of ν > 30.
The following are the plots of the t cumulative distribution function with the same values of ν as the pdf plots above.
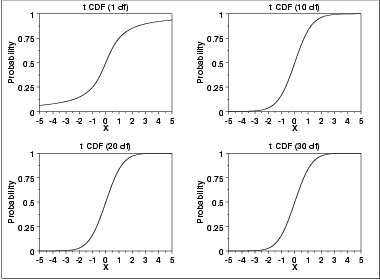
The following are the plots of the t percent point function with the same values of ν as the pdf plots above.
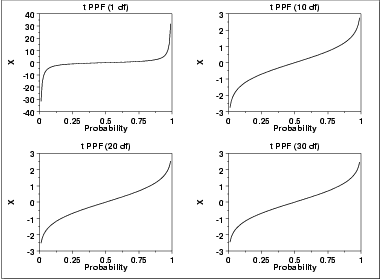
| Mean | 0 (It is undefined for ν equal to 1.) |
| Median | 0 |
| Mode | 0 |
| Range | \(-\infty \mbox{ to } \infty\) |
| Standard Deviation |
\( \sqrt{\frac {\nu} {(\nu - 2)}} \)
It is undefined for ν equal to 1 or 2. |
| Coefficient of Variation | Undefined |
| Skewness | 0. It is undefined for ν less than or equal to 3. However, the t distribution is symmetric in all cases. |
| Kurtosis |
\( \frac {3(\nu-2)} {(\nu - 4)} \)
It is undefined for ν less than or equal to 4. |

