1.3. EDA Techniques
1.3.6. Probability Distributions
1.3.6.6. Gallery of Distributions
1.3.6.6.6. |
Chi-Square Distribution |
\( f(x) = \frac{e^{\frac{-x} {2}}x^{\frac{\nu} {2} - 1}} {2^{\frac{\nu} {2}}\Gamma(\frac{\nu} {2}) } \;\;\;\;\;\;\; \mbox{for} \; x \ge 0 \)
where ν is the shape parameter and Γ is the gamma function. The formula for the gamma function is
\( \Gamma(a) = \int_{0}^{\infty} {t^{a-1}e^{-t}dt} \)
In a testing context, the chi-square distribution is treated as a "standardized distribution" (i.e., no location or scale parameters). However, in a distributional modeling context (as with other probability distributions), the chi-square distribution itself can be transformed with a location parameter, μ, and a scale parameter, σ.
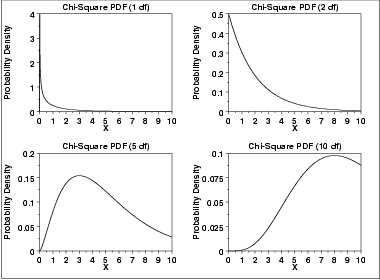
The following is the plot of the chi-square probability density function for 4 different values of the shape parameter.
\( F(x) = \frac{\gamma(\frac{\nu} {2},\frac{x} {2})} {\Gamma(\frac{\nu} {2})} \;\;\;\;\;\;\; \mbox{for} \; x \ge 0 \)
where Γ is the gamma function defined above and γ is the incomplete gamma function. The formula for the incomplete gamma function is
\( \Gamma_{x}(a) = \int_{0}^{x} {t^{a-1}e^{-t}dt} \)
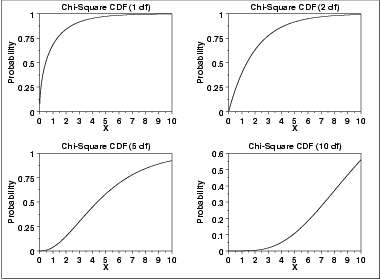
The following is the plot of the chi-square cumulative distribution function with the same values of ν as the pdf plots above.
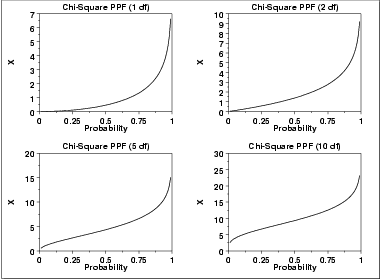
The following is the plot of the chi-square percent point function with the same values of ν as the pdf plots above.
| Mean | ν |
| Median | approximately ν - 2/3 for large ν |
| Mode | \( \nu - 2 \;\;\;\;\;\;\; \mbox{for} \; \nu > 2 \) |
| Range | 0 to \(\infty\) |
| Standard Deviation | \( \sqrt{2\nu} \) |
| Coefficient of Variation | \( \sqrt{\frac{2} {\nu}} \) |
| Skewness | \( \frac{2^{1.5} } {\sqrt{\nu}} \) |
| Kurtosis | \( 3 + \frac{12} {\nu} \) |

