1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.27. Spectral Plot
1.3.3.27.2. |
Spectral Plot: Strong Autocorrelation and Autoregressive Model |
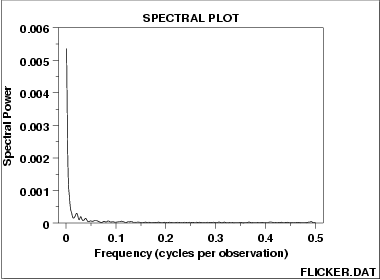
- Strong dominant peak near zero.
- Peak decays rapidly towards zero.
- An autoregressive model is an appropriate model.
-
\[ Y_{i} = A_0 + A_1*Y_{i-1} + E_{i} \]
Such estimation can be done by linear regression or by fitting a Box-Jenkins autoregressive (AR) model.
The residual standard deviation for this autoregressive model will be much smaller than the residual standard deviation for the default model
-
\[ Y_{i} = A_0 + E_{i} \]
Then the system should be reexamined to find an explanation for the strong autocorrelation. Is it due to the
- phenomenon under study; or
- drifting in the environment; or
- contamination from the data acquisition system (DAS)?

