1. Exploratory Data Analysis
1.4. EDA Case Studies
1.4.2. Case Studies
1.4.2.6. Filter Transmittance

1.4.2.6.3.

Quantitative Output and Interpretation

Summary Statistics

As a first step in the analysis, common summary statistics are computed from the data.

      Sample size  = 50
      Mean         =  2.0019
      Median       =  2.0018
      Minimum      =  2.0013  
      Maximum      =  2.0027  
      Range        =  0.0014  
      Stan. Dev.   =  0.0004  

Location

One way to quantify a change in location over time is to fit a straight line to the data using an index variable as the independent variable in the regression. For our data, we assume that data are in sequential run order and that the data were collected at equally spaced time intervals. In our regression, we use the index variable X = 1, 2, ..., N, where N is the number of observations. If there is no significant drift in the location over time, the slope parameter should be zero.

      Coefficient     Estimate     Stan. Error      t-Value
          B0           2.00138      0.9695E-04   0.2064E+05
          B1         0.185E-04      0.3309E-05        5.582
 
      Residual Standard Deviation = 0.3376404E-03
      Residual Degrees of Freedom = 48

The slope parameter, B₁, has a t value of 5.582, which is statistically significant. Although the estimated slope, 0.185E-04, is nearly zero, the range of data (2.0013 to 2.0027) is also very small. In this case, we conclude that there is drift in location, although it is relatively small.

Variation

One simple way to detect a change in variation is with a Bartlett test after dividing the data set into several equal sized intervals. However, the Bartlett test is not robust for non-normality. Since the normality assumption is questionable for these data, we use the alternative Levene test. In particular, we use the Levene test based on the median rather the mean. The choice of the number of intervals is somewhat arbitrary, although values of four or eight are reasonable. We will divide our data into four intervals.

      H0:  σ12 = σ22 = σ32 = σ42 
      Ha:  At least one σi2 is not equal to the others.

      Test statistic:  W = 0.971
      Degrees of freedom:  k - 1 = 3
      Significance level:  α = 0.05
      Critical value:  Fα,k-1,N-k = 2.806
      Critical region:  Reject H0 if W > 2.806

In this case, since the Levene test statistic value of 0.971 is less than the critical value of 2.806 at the 5 % level, we conclude that there is no evidence of a change in variation.

Randomness

There are many ways in which data can be non-random. However, most common forms of non-randomness can be detected with a few simple tests. The lag plot in the 4-plot in the previous seciton is a simple graphical technique.

One check is an autocorrelation plot that shows the autocorrelations for various lags. Confidence bands can be plotted at the 95 % and 99 % confidence levels. Points outside this band indicate statistically significant values (lag 0 is always 1).

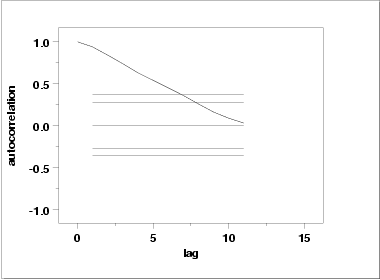
The lag 1 autocorrelation, which is generally the one of most interest, is 0.93. The critical values at the 5 % level are -0.277 and 0.277. This indicates that the lag 1 autocorrelation is statistically significant, so there is strong evidence of non-randomness.

A common test for randomness is the runs test.

      H0:  the sequence was produced in a random manner
      Ha:  the sequence was not produced in a random manner  

      Test statistic:  Z = -5.3246
      Significance level:  α = 0.05
      Critical value:  Z1-α/2 = 1.96 
      Critical region:  Reject H0 if |Z| > 1.96 

Because the test statistic is outside of the critical region, we reject the null hypothesis and conclude that the data are not random.

Distributional Analysis

Since we rejected the randomness assumption, the distributional tests are not meaningful. Therefore, these quantitative tests are omitted. We also omit Grubbs' outlier test since it also assumes the data are approximately normally distributed.

Univariate Report

It is sometimes useful and convenient to summarize the above results in a report.

  
 Analysis for filter transmittance data
  
 1: Sample Size                           = 50
  
 2: Location
    Mean                                  = 2.001857
    Standard Deviation of Mean            = 0.00006
    95% Confidence Interval for Mean      = (2.001735,2.001979)
    Drift with respect to location?       = NO
  
 3: Variation
    Standard Deviation                    = 0.00043
    95% Confidence Interval for SD        = (0.000359,0.000535)
    Change in variation?
    (based on Levene's test on quarters
    of the data)                          = NO
  
 4: Distribution
    Distributional tests omitted due to
    non-randomness of the data
  
 5: Randomness
    Lag One Autocorrelation               = 0.937998
    Data are Random?
      (as measured by autocorrelation)    = NO
  
 6: Statistical Control
    (i.e., no drift in location or scale,
    data are random, distribution is 
    fixed, here we are testing only for
    normal)
    Data Set is in Statistical Control?   = NO
  
 7: Outliers?
    (Grubbs' test omitted)                = NO