2.4.3.2. 2-level nested design

2. Measurement Process Characterization
2.4. Gauge R & R studies
2.4.3. Data collection for time-related sources of variability

2.4.3.2. 2-level nested design

Check standard measurements for estimating time-dependent sources of variability

Measurements on a check standard are recommended for studying the effect of sources of variability that manifest themselves over time. Data collection and analysis are straightforward, and there is no reason to estimate interaction terms when dealing with time-dependent errors. The measurements can be made at one of two levels. Two levels should be sufficient for characterizing most measurement systems. Three levels are recommended for measurement systems for which sources of error are not well understood and have not previously been studied.

Time intervals in a nested design

The following levels are based on the characteristics of many measurement systems and should be adapted to a specific measurement situation as needed.

Level-1 Measurements taken over a short term to estimate gauge precision
Level-2 Measurements taken over days (of other appropriate time increment)

Definition of number of measurements at each level

The following symbols are defined for this chapter:

Level-1 J (J > 1) repetitions
Level-2 K (K > 2) days

Schedule for making measurements

A schedule for making check standard measurements over time (once a day, twice a week, or whatever is appropriate for sampling all conditions of measurement) should be set up and adhered to. The check standard measurements should be structured in the same way as values reported on the test items. For example, if the reported values are averages of two repetitions made within 5 minutes of each other, the check standard values should be averages of the two measurements made in the same manner.

Exception

One exception to this rule is that there should be at least J = 2 repetitions per day, etc. Without this redundancy, there is no way to check on the short-term precision of the measurement system.

Depiction of schedule for making check standard measurements with 4 repetitions per day over K days on the surface of a silicon wafer

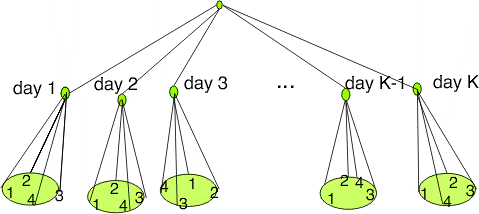K days - 4 repetitions

2-level design for check standard measurements

Operator considerations

The measurements should be taken with ONE operator. Operator is not usually a consideration with automated systems. However, systems that require decisions regarding line edge or other feature delineations may be operator dependent.

Case Study: Resistivity check standard

Results should be recorded along with pertinent environmental readings and identifications for significant factors. The best way to record this information is in one file with one line or row (on a spreadsheet) of information in fixed fields for each check standard measurement.

Data analysis of gauge precision

The check standard measurements are represented by $$Y_{kj}(k=1, \,\ldots, \, K, \,\, j=1, \,\ldots, \, J) \,\, ,$$ for the jth repetition on the kth day. The mean for the kth day is $$\overline{Y}_{k \, \small{\bullet}} = \frac{1}{J}\sum_{j=1}^{J} Y_{kj} \,\, ,$$ and the (level-1) standard deviation for gauge precision with $ \nu = J -1 $ degrees of freedom is
$${\large s}_k = \sqrt{\frac{1}{J-1} \sum_{j=1}^{J} ( Y_{kj} - \overline{Y}_{k \, \small{\bullet}} ) ^2} \,\,\,\, . $$

Pooling increases the reliability of the estimate of the standard deviation

The pooled level-1 standard deviation with $ \nu = K(J-1) $ degrees of freedom is $${\large s}_1 = \sqrt{\frac{1}{K} \sum_{k=1}^{K} {\large s}_k^2} \,\,\,\, . $$

Data analysis of process (level-2) standard deviation

The level-2 standard deviation of the check standard represents the process variability. It is computed with $ \nu = K - 1 $ degrees of freedom as: $${\large s}_{chkstd} = {\large s}_2 = \sqrt{\frac{1}{K-1} \sum_{k=1}^{K} \left( \overline{Y}_{k \, \small{\bullet}} - \overline{Y}_{\small{\bullet} \small{\bullet}} \right) ^2} \,\, ,$$ where $$\overline{Y}_{\small{\bullet} \small{\bullet}} = \frac{1}{K} \sum_{k=1}^{K} \overline{Y}_{k \, \small{\bullet}} \,\, .$$

Relationship to uncertainty for a test item

The standard deviation that defines the uncertainty for a single measurement on a test item, often referred to as the reproducibility standard deviation (ASTM), is given by $$ {\large s}_R = \sqrt{{\large s}_{days}^2 + {\large s}_1^2} = \sqrt{{\large s}_2^2 + \frac{J-1}{J} {\large s}_1^2} \,\, . $$ There may be other sources of uncertainty in the measurement process that must be accounted for in a formal analysis of uncertainty.