2.
Measurement Process Characterization
2.4.
Gauge R & R studies
2.4.4.
|
Analysis of variability
|
|
|
Analysis of variability from a nested design
|
The purpose of this section is to show the effect of various levels of
time-dependent effects on the variability of the measurement process
with standard deviations for each level of a 3-level nested design.
The graph below depicts possible scenarios for a 2-level design
(short-term repetitions and days) to illustrate the concepts.
|
|
Depiction of 2 measurement processes with the same short-term
variability over 6 days where process 1 has large between-day
variability and process 2 has negligible between-day variability
|
Process 1 Process 2
Large between-day variability Small between-day variability
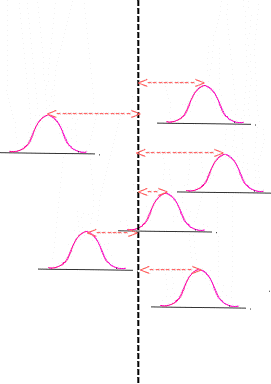
Distributions of short-term measurements over 6 days
where distances from centerlines illustrate between-day variability
|
|
Hint on using tabular method of analysis
|
An easy way to begin is with a 2-level
table with J columns and K rows for the
repeatability/reproducibility measurements and proceed as follows:
- Compute an average for each row and put it in the J + 1
column.
- Compute the level-1 (repeatability) standard deviation for each
row and put it in the J + 2 column.
- Compute the grand average and the level-2 standard deviation
from data in the J + 1 column.
- Repeat the table for each of the L runs.
- Compute the level-3 standard deviation from the L grand
averages.
|
|
Level-1: LK repeatability standard deviations can be
computed from the data
|
The measurements from the nested design are denoted by
$$Y_{lkj}(l = 1, \, \ldots, \, L, \,\, k=1, \,\ldots, \, K, \,\, j=1, \,\ldots, \, J) \,\, .$$
Equations corresponding to the tabular analysis are shown below.
Level-1 repeatability standard deviations,
\( {\large s}_{1lk} \) ,
are pooled over the K days and
L runs. Individual standard deviations with (J - 1)
degrees of freedom each are computed from J repetitions as
$$ s_{1lk} = \sqrt{\frac{1}{J-1} \sum_{j=1}^{J}{(Y_{lkj} - \overline{Y}_{lk{\small \, \bullet}})^2}} $$
where
$$ \overline{Y}_{lk{\small \, \bullet}} = \frac{1}{J}\sum_{j=1}^{J}{\overline{Y}_{lkj}} \,\, . $$
|
|
Level-2: L reproducibility standard deviations can be computed from
the data
|
The level-2 standard deviation, \( {\large s}_{2l} \),
is pooled
over the L runs.
Individual standard deviations with (K - 1) degrees of freedom
each are computed from K daily averages as
$$ {\large s}_{2l} = \sqrt{\frac{1}{K-1} \sum_{k=1}^{K}{\left( Y_{lk{\small \, \bullet}} - \overline{Y}_{l{\small \, \bullet \bullet}} \right)^2}} $$
where
$$ \overline{Y}_{l{\small \, \bullet \bullet}} = \frac{1}{K}\sum_{k=1}^{K}{\overline{Y}_{lk {\small \, \bullet}}} \,\,\, .$$
|
|
Level-3: A single global standard deviation can be computed from
the L-run averages
|
A level-3 standard deviation with (L - 1) degrees of freedom
is computed from the L-run averages as
$$ {\large s}_{3} = \sqrt{\frac{1}{L-1} \sum_{l=1}^{L}{\left( Y_{l{\small \, \bullet \bullet}} - \overline{Y}_{{\small \bullet \bullet \bullet}} \right)^2}} $$
where
$$ \overline{Y}_{{\small \bullet \bullet \bullet}} = \frac{1}{L}\sum_{l=1}^{L}{\overline{Y}_{l {\small \, \bullet \bullet}}} \,\,\, . $$
|
|
Relationship to uncertainty
for a test item
|
The standard deviation that defines the uncertainty for a single
measurement on a test item is given by
$$ {\large s}_R = \sqrt{{\large s}_{runs}^2 + {\large s}_{days}^2 + {\large s}_1^2}
= \sqrt{{\large s}_3^2 + \frac{K-1}{K} {\large s}_2^2 + \frac{J-1}{J} {\large s}_1^2} \,\, , $$
where the pooled values, \( {\large s}_1 \) and
\( {\large s}_2 \), are the usual
$$ {\large s}_1 = \sqrt{\frac{\sum_{l=1}^{L}{\sum_{k=1}^{K}{{\large s}_{1lk}^{2}}}}{LK}} $$
and
$$ {\large s}_2 = \sqrt{\frac{1}{L} \sum_{l=1}^{L}{{\large s}_{2l}^{2}}} \,\,\, . $$
The time-dependent components can be computed individually as:
$$ {\large s}_{runs} = \sqrt{{\large s}_3^2 - \frac{1}{K} {\large s_2^2}} $$
$$ {\large s}_{days} = \sqrt{{\large s}_2^2 - \frac{1}{J} {\large s_1^2}} \,\,\, .$$
There may be other sources of uncertainty in the measurement process
that must be accounted for in a formal
analysis of uncertainty.
|
