Next Page Previous Page Home Tools & Aids Search Handbook
6. Process or Product Monitoring and Control
6.2. Test Product for Acceptability: Lot Acceptance Sampling

6.2.4.

What is Double Sampling?
Double Sampling Plans
How double sampling plans work Double and multiple sampling plans were invented to give a questionable lot another chance. For example, if in double sampling the results of the first sample are not conclusive with regard to accepting or rejecting, a second sample is taken. Application of double sampling requires that a first sample of size n1 is taken at random from the (large) lot. The number of defectives is then counted and compared to the first sample's acceptance number a1 and rejection number r1. Denote the number of defectives in sample 1 by d1 and in sample 2 by d2, then:
    If d1 <= a1, the lot is accepted.
    If d1 >= r1, the lot is rejected.
    If a1 < d1 < r1, a second sample is taken.
If a second sample of size n2 is taken, the number of defectives, d2, is counted. The total number of defectives is D2 = d1 + d2. Now this is compared to the acceptance number a2 and the rejection number r2 of sample 2. In double sampling, r2 = a2 + 1 to ensure a decision on the sample.
    If D2 <= a2, the lot is accepted.
    If D2 >= r2, the lot is rejected.
Design of a Double Sampling Plan
Design of a double sampling plan The parameters required to construct the OC curve are similar to the single sample case. The two points of interest are (p1, 1-alpha) and (p2, beta, where p1 is the lot fraction defective for plan 1 and p2 is the lot fraction defective for plan 2. As far as the respective sample sizes are concerned, the second sample size must be equal to, or an even multiple of, the first sample size.

There exist a variety of tables that assist the user in constructing double and multiple sampling plans. The index to these tables is the p2/p1 ratio, where p2 > p1. One set of tables, taken from the Army Chemical Corps Engineering Agency for alpha = .05 and beta = .10, is given below:

Tables for n1 = n2
  accept   approximation values
R = numbers   of pn1 for
p2/p1 c1 c2 P = .95 P = .10
11.90 0 1 0.21 2.50
7.54 1 2 0.52 3.92
6.79 0 2 0.43 2.96
5.39 1 3 0.76 4.11
4.65 2 4 1.16 5.39
4.25 1 4 1.04 4.42
3.88 2 5 1.43 5.55
3.63 3 6 1.87 6.78
3.38 2 6 1.72 5.82
3.21 3 7 2.15 6.91
3.09 4 8 2.62 8.10
2.85 4 9 2.90 8.26
2.60 5 11 3.68 9.56
2.44 5 12 4.00 9.77
2.32 5 13 4.35 10.08
2.22 5 14 4.70 10.45
2.12 5 16 5.39 11.41

Tables for n2 = 2n1
  accept   approximation values
R = numbers   of pn1 for
p2/p1 c1 c2 P = .95 P = .10
14.50 0 1 0.16 2.32
8.07 0 2 0.30 2.42
6.48 1 3 0.60 3.89
5.39 0 3 0.49 2.64
5.09 0 4 0.77 3.92
4.31 1 4 0.68 2.93
4.19 0 5 0.96 4.02
3.60 1 6 1.16 4.17
3.26 1 8 1.68 5.47
2.96 2 10 2.27 6.72
2.77 3 11 2.46 6.82
2.62 4 13 3.07 8.05
2.46 4 14 3.29 8.11
2.21 3 15 3.41 7.55
1.97 4 20 4.75 9.35
1.74 6 30 7.45 12.96

Example
Example of a double sampling plan We wish to construct a double sampling plan according to
    p1 = 0.01     alpha = 0.05     p2 = 0.05     beta = 0.10     and n1 = n2
The plans in the corresponding table are indexed on the ratio
    R = p2/p1 = 5
We find the row whose R is closet to 5. This is the 5th row (R = 4.65). This gives c1 = 2 and c2 = 4. The value of n1 is determined from either of the two columns labeled pn1.

The left holds alpha constant at 0.05 (P = 0.95 = 1 - alpha) and the right holds beta constant at 0.10. (P = 0.10). Then holding alpha constant we find pn1 = 1.16 so n1 = 1.16/p1 = 116. And, holding beta constant we find pn1 = 5.39, so n1 = 5.39/p2 = 108. Thus the desired sampling plan is

    n1 = 108     c1 = 2     n2 = 108     c2 = 4
If we opt for n2 = 2n1, and follow the same procedure using the appropriate table, the plan is:
    n1 = 77     c1 = 1     n2 = 154     c2 = 4

The first plan needs less samples if the number of defectives in sample 1 is greater than 2, while the second plan needs less samples if the number of defectives in sample 1 is less than 2.

ASN Curve for a Double Sampling Plan
Construction of the ASN curve Since when using a double sampling plan the sample size depends on whether or not a second sample is required, an important consideration for this kind of sampling is the Average Sample Number (ASN) curve. This curve plots the ASN versus p', the true fraction defective in an incoming lot.

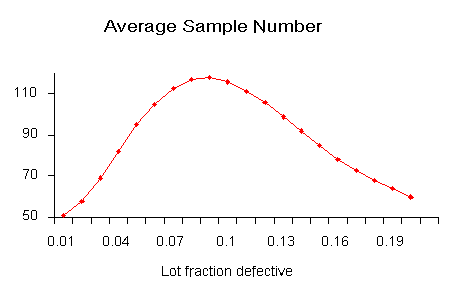
We will illustrate how to calculate the ASN curve with an example. Consider a double-sampling plan n1 = 50, c1= 2, n2 = 100, c2 = 6, where n1 is the sample size for plan 1, with accept number c1, and n2, c2, are the sample size and accept number, respectively, for plan 2.

Let p' = .06. Then the probability of acceptance on the first sample, which is the chance of getting two or less defectives, is .416 (using binomial tables). The probability of rejection on the second sample, which is the chance of getting more than six defectives, is (1-.971) = .029. The probability of making a decision on the first sample is .445, equal to the sum of .416 and .029. With complete inspection of the second sample, the average size sample is equal to the size of the first sample times the probability that there will be only one sample plus the size of the combined samples times the probability that a second sample will be necessary. For the sampling plan under consideration, the ASN with complete inspection of the second sample for a p' of .06 is

    50(.445) + 150(.555) = 106
The general formula for an average sample number curve of a double-sampling plan with complete inspection of the second sample is
    ASN = n1P1 + (n1 + n2)(1 - P1) = n1 + n2(1 - P1)
where P1 is the probability of a decision on the first sample. The graph below shows a plot of the ASN versus p'.
The ASN curve for a double sampling plan Plot of Average Sample Number versus Lot Fraction Defective
Home Tools & Aids Search Handbook Previous Page Next Page