6.
Process or Product Monitoring and Control
6.2.
Test Product for Acceptability: Lot Acceptance
Sampling
6.2.7.
|
What is Skip Lot Sampling?
|
|
|
Skip Lot Sampling
|
Skip Lot sampling means that only a fraction of the submitted
lots are inspected. This mode of sampling is of the cost-saving
variety in terms of time and effort. However skip-lot sampling
should only be used when it has been demonstrated that the quality
of the submitted product is very good.
|
|
Implementation of skip-lot sampling plan
|
A skip-lot sampling plan is implemented as follows:
- Design a single sampling plan by
specifying the alpha and beta risks and the
consumer/producer's risks. This plan is called
"the reference sampling plan".
- Start with normal lot-by-lot inspection, using the reference
plan.
- When a pre-specified number, \(i\)
of consecutive lots
are accepted, switch to inspecting only a fraction \(f\)
of the lots. The selection of the members of that fraction
is done at random.
- When a lot is rejected return to normal inspection.
|
|
The \(f\) and \(i\) parameters
|
The parameters \(f\) and \(i\)
are essential to calculating
the probability of acceptance for a skip-lot sampling plan.
In this scheme, \(i\),
called the clearance number, is
a positive integer and the sampling fraction \(f\)
is such that \(0 < f < 1\).
Hence, when \(f=1\)
there is no longer skip-lot sampling. The calculation of the
acceptance probability for the skip-lot sampling plan is performed
via the following formula
$$ P_a(f,i) = \frac{fP + (1-f)P^i}{f + (1-f)P^i} \, ,$$
where \(P\)
is the probability of accepting a lot with a given
proportion of incoming defectives \(p\),
from the
OC curve
of the single sampling plan.
The following relationships hold:
for a given \(i\),
the smaller is \(f\)
the greater is \(P_a\),
for a given \(f\),
the smaller is \(i\),
the greater is \(P_a\).
|
|
Illustration of a skip lot sampling plan
|
An illustration of a a skip-lot sampling plan is given below.
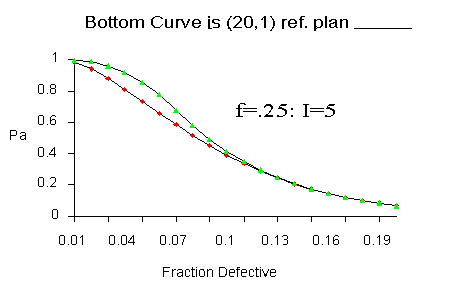
|
|
ASN of skip-lot sampling plan
|
An important property of skip-lot sampling plans is the average
sample number
(ASN).
The ASN
of a skip-lot sampling plan is
$$ \mbox{ASN}_{skip-lot} = (F)(\mbox{ASN}_{reference}) \, , $$
where \(F\)
is defined by
$$ F = \frac{f}{(1-f)P_i + f} \, .$$
Therefore, since \(0 < F < 1\),
it follows that the ASN
of skip-lot sampling is smaller than the ASN
of the reference sampling plan.
In summary, skip-lot sampling is preferred when the quality of the
submitted lots is excellent and the supplier can demonstrate a
proven track record.
|


