Next Page Previous Page Home Tools & Aids Search Handbook
4. Process Modeling
4.4. Data Analysis for Process Modeling
4.4.5. If my current model does not fit the data well, how can I improve it?

4.4.5.2.

Accounting for Non-Constant Variation Across the Data
Two Basic Approaches: Transformation and Weighting There are two basic approaches to obtaining improved parameter estimators for data in which the standard deviation of the error is not constant across all combinations of predictor variable values:
  1. transforming the data so it meets the standard assumptions, and
  2. using weights in the parameter estimation to account for the unequal standard deviations.
Both methods work well in a wide range of situations. The choice of which to use often hinges on personal preference because in many engineering and industrial applications the two methods often provide practically the same results. In fact, in most experiments there is usually not enough data to determine which of the two models works better. Sometimes, however, when there is scientific information about the nature of the model, one method or the other may be preferred because it is more consistent with an existing theory. In other cases, the data may make one of the methods more convenient to use than the other.
Using Transformations The basic steps for using transformations to handle data with unequal subpopulation standard deviations are:
  1. Transform the response variable to equalize the variation across the levels of the predictor variables.
  2. Transform the predictor variables, if necessary, to attain or restore a simple functional form for the regression function.
  3. Fit and validate the model in the transformed variables.
  4. Transform the predicted values back into the original units using the inverse of the transformation applied to the response variable.
Typical Transformations for Stabilization of Variation Appropriate transformations to stabilize the variability may be suggested by scientific knowledge or selected using the data. Three transformations that are often effective for equalizing the standard deviations across the values of the predictor variables are:
  1. \(\sqrt{y}\),
  2. \(\ln{(y)}\) (note: the base of the logarithm does not really matter), and

  3. \(\frac{1}{y}\).
Other transformations can be considered, of course, but in a surprisingly wide range of problems one of these three transformations will work well. As a result, these are good transformations to start with, before moving on to more specialized transformations.
Modified Pressure / Temperature Example To illustrate how to use transformations to stabilize the variation in the data, we will return to the modified version of the Pressure/Temperature example. The residuals from a straight-line fit to that data clearly showed that the standard deviation of the measurements was not constant across the range of temperatures.
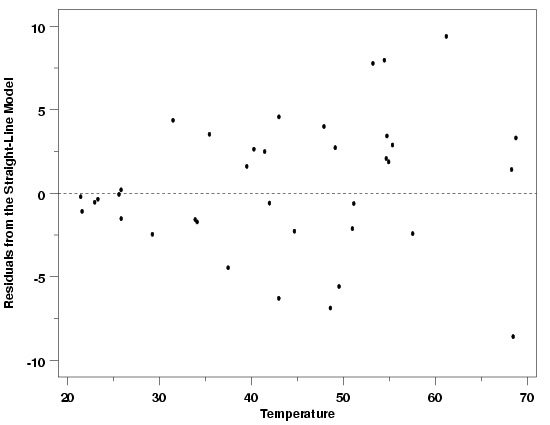
Residuals from Modified Pressure Data residuals from modified pressure/temperature example with straight line fit
Stabilizing the Variation The first step in the process is to compare different transformations of the response variable, pressure, to see which one, if any, stabilizes the variation across the range of temperatures. The straight-line relationship will not hold for all of the transformations, but at this stage of the process that is not a concern. The functional relationship can usually be corrected after stabilizing the variation. The key for this step is to find a transformation that makes the uncertainty in the data approximately the same at the lowest and highest temperatures (and in between). The plot below shows the modified Pressure/Temperature data in its original units, and with the response variable transformed using each of the three typical transformations. Remember you can click on the plot to see a larger view for easier comparison.
Transformations of the Pressure Transformations of the Pressure
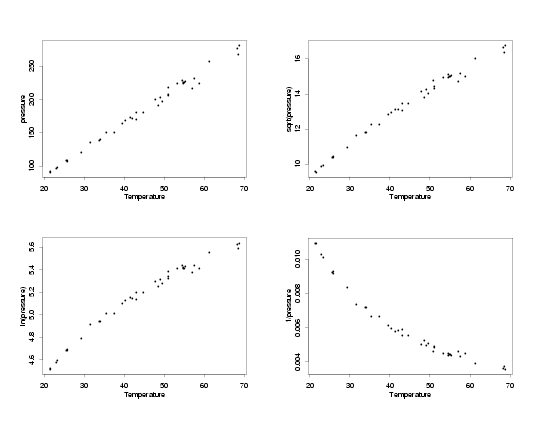
Inverse Pressure Has Constant Variation After comparing the effects of the different transformations, it looks like using the inverse of the pressure will make the standard deviation approximately constant across all temperatures. However, it is somewhat difficult to tell how the standard deviations really compare on a plot of this size and scale. To better see the variation, a full-sized plot of temperature versus the inverse of the pressure is shown below. In that plot it is easier to compare the variation across temperatures. For example, comparing the variation in the pressure values at a temperature of about 25 with the variation in the pressure values at temperatures near 45 and 70, this plot shows about the same level of variation at all three temperatures. It will still be critical to look at residual plots after fitting the model to the transformed variables, however, to really see whether or not the transformation we've chosen is effective. The residual scale is really the only scale that can reveal that level of detail.
Enlarged View of Temperature Versus 1/Pressure Enlarged View of Temperature Versus 1/Pressure
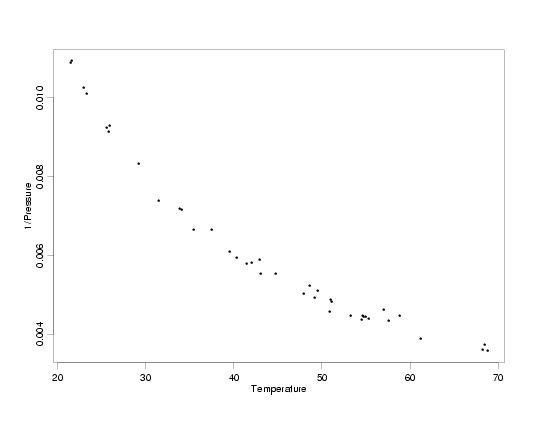
Transforming Temperature to Linearity Having found a transformation that appears to stabilize the standard deviations of the measurements, the next step in the process is to find a transformation of the temperature that will restore the straight-line relationship, or some other simple relationship, between the temperature and pressure. The same three basic transformations that can often be used to stabilize the variation are also usually able to transform the predictor to restore the original relationship between the variables. Plots of the temperature and the three transformations of the temperature versus the inverse of the pressure are shown below.
Transformations of the Temperature Tranformations of the Temperature
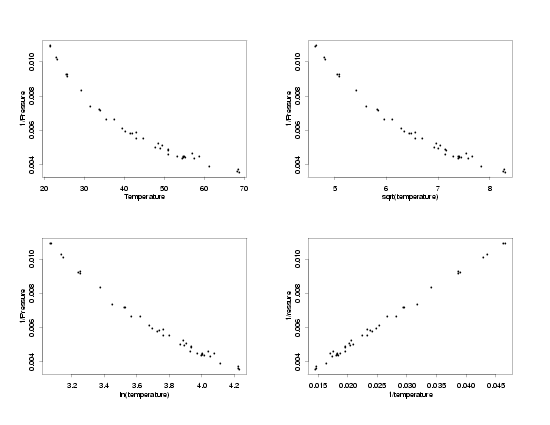
  Comparing the plots of the various transformations of the temperature versus the inverse of the pressure, it appears that the straight-line relationship between the variables is restored when the inverse of the temperature is used. This makes intuitive sense because if the temperature and pressure are related by a straight line, then the same transformation applied to both variables should change them both similarly, retaining their original relationship. Now, after fitting a straight line to the transformed data, the residuals plotted versus both the transformed and original values of temperature indicate that the straight-line model fits the data and that the random variation no longer increases with increasing temperature. Additional diagnostic plots of the residuals confirm that the model fits the data well.
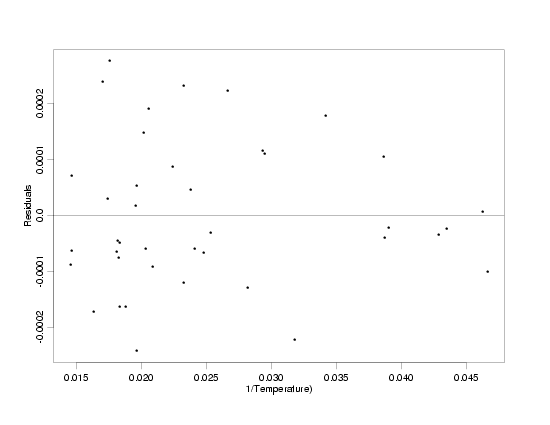
Residuals From the Fit to the Transformed Data residuals from the fit to the transformed data versus 1/temperature
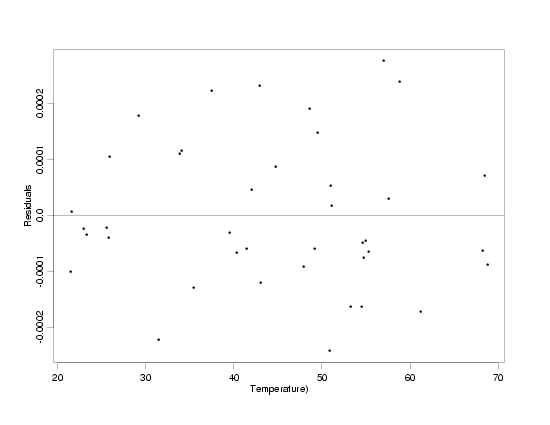
residuals from the fit to the transformed data versus temperature
Using Weighted Least Squares As discussed in the overview of different methods for building process models, the goal when using weighted least squares regression is to ensure that each data point has an appropriate level of influence on the final parameter estimates. Using the weighted least squares fitting criterion, the parameter estimates are obtained by minimizing $$ Q = \sum_{i=1}^{n} \ w_i \left[ y_i - f(\vec{x}_i;\hat{\vec{\beta}}) \right]^2 \, . $$ Optimal results, which minimize the uncertainty in the parameter estimators, are obtained when the weights, \(w_i\), used to estimate the values of the unknown parameters are inversely proportional to the variances at each combination of predictor variable values: $$ w_i \propto \frac{1}{\sigma^2_i} \, .$$ Unfortunately, however, these optimal weights, which are based on the true variances of each data point, are never known. Estimated weights have to be used instead. When estimated weights are used, the optimality properties associated with known weights no longer strictly apply. However, if the weights can be estimated with high enough precision, their use can significantly improve the parameter estimates compared to the results that would be obtained if all of the data points were equally weighted.
Direct Estimation of Weights If there are replicates in the data, the most obvious way to estimate the weights is to set the weight for each data point equal to the reciprocal of the sample variance obtained from the set of replicate measurements to which the data point belongs. Mathematically, this would be $$ w_{ij} = \frac{1}{\hat{\sigma}^2_i} = \left[\frac{\sum_{j=1}^{n_i}(y_{ij}-\bar{y}_i)^2}{n_i-1}\right]^{-1} $$ where
  • \(w_{ij}\) are the weights indexed by their predictor variable levels and replicate measurements,
  • \(i\) indexes the unique combinations of predictor variable values,
  • \(j\) indexes the replicates within each combination of predictor variable values,
  • \(\hat{\sigma_i}\) is the sample standard deviation of the response variable at the ith combination of predictor variable values,
  • \(n_i\) is the number of replicate observations at the ith combination of predictor variable values,
  • \(y_{ij}\) are the individual data points indexed by their predictor variable levels and replicate measurements,
  • \(\bar{y}_i\) is the mean of the responses at the ith combination of predictor variable levels.
Unfortunately, although this method is attractive, it rarely works well. This is because when the weights are estimated this way, they are usually extremely variable. As a result, the estimated weights do not correctly control how much each data point should influence the parameter estimates. This method can work, but it requires a very large number of replicates at each combination of predictor variables. In fact, if this method is used with too few replicate measurements, the parameter estimates can actually be more variable than they would have been if the unequal variation were ignored.
A Better Strategy for Estimating the Weights A better strategy for estimating the weights is to find a function that relates the standard deviation of the response at each combination of predictor variable values to the predictor variables themselves. This means that if $$ \hat{\sigma}_i^2 \approx g(\vec{x}_i;\vec{\gamma}) $$ (denoting the unknown parameters in the function \(g\) by \(\vec{\gamma}\)), then the weights can be set to $$ w_{ij} = \frac{1}{g(\vec{x}_i;\hat{\vec{\gamma}})} \, . $$ This approach to estimating the weights usually provides more precise estimates than direct estimation because fewer quantities have to be estimated and there is more data to estimate each one.
Estimating Weights Without Replicates If there are only very few or no replicate measurements for each combination of predictor variable values, then approximate replicate groups can be formed so that weights can be estimated. There are several possible approaches to forming the replicate groups.
  1. One method is to manually form the groups based on plots of the response against the predictor variables. Although this allows a lot of flexibility to account for the features of a specific data set, it often impractical. However, this approach may be useful for relatively small data sets in which the spacing of the predictor variable values is very uneven.

  2. Another approach is to divide the data into equal-sized groups of observations after sorting by the values of the response variable. It is important when using this approach not to make the size of the replicate groups too large. If the groups are too large, the standard deviations of the response in each group will be inflated because the approximate replicates will differ from each other too much because of the deterministic variation in the data. Again, plots of the response variable versus the predictor variables can be used as a check to confirm that the approximate sets of replicate measurements look reasonable.

  3. A third approach is to choose the replicate groups based on ranges of predictor variable values. That is, instead of picking groups of a fixed size, the ranges of the predictor variables are divided into equal size increments or bins and the responses in each bin are treated as replicates. Because the sizes of the groups may vary, there is a tradeoff in this case between defining the intervals for approximate replicates to be too narrow or too wide. As always, plots of the response variable against the predictor variables can serve as a guide.
Although the exact estimates of the weights will be somewhat dependent on the approach used to define the replicate groups, the resulting weighted fit is typically not particularly sensitive to small changes in the definition of the weights when the weights are based on a simple, smooth function.
Power Function Model for the Weights One particular function that often works well for modeling the variances is a power of the mean at each combination of predictor variable values, $$ \begin{array}{ccl} \hat{\sigma}_i^2 & \approx & \gamma_1\mu_i^{\gamma_2} \\ & & \\ & = & \gamma_1f(\vec{x}_i;\vec{\beta})^{\gamma_2} \, . \end{array} $$ Iterative procedures for simultaneously fitting a weighted least squares model to the original data and a power function model for the weights are discussed in Carroll and Ruppert (1988), and Ryan (1997).
Fitting the Model for Estimation of the Weights When fitting the model for the estimation of the weights, $$ \hat{\sigma}_i^2 = g(\vec{x}_i;\vec{\gamma}) + g(\vec{x}_i;\vec{\gamma})\varepsilon \, ,$$ it is important to note that the usual regression assumptions do not hold. In particular, the variation of the random errors is not constant across the different sets of replicates and their distribution is not normal. However, this can be often be accounted for by using transformations (the ln transformation often stabilizes the variation), as described above.
Validating the Model for Estimation of the Weights Of course, it is always a good idea to check the assumptions of the analysis, as in any model-building effort, to make sure the model of the weights seems to fit the weight data reasonably well. The fit of the weights model often does not need to meet all of the usual standards to be effective, however.
Using Weighted Residuals to Validate WLS Models Once the weights have been estimated and the model has been fit to the original data using weighted least squares, the validation of the model follows as usual, with one exception. In a weighted analysis, the distribution of the residuals can vary substantially with the different values of the predictor variables. This necessitates the use of weighted residuals [Graybill and Iyer (1994)] when carrying out a graphical residual analysis so that the plots can be interpreted as usual. The weighted residuals are given by the formula $$ e_{ij} = \sqrt{w_{ij}} \, \left[y_{ij} - f(\vec{x}_i;\hat{\vec{\beta}})\right] \, .$$ It is important to note that most statistical software packages do not compute and return weighted residuals when a weighted fit is done, so the residuals will usually have to be weighted manually in an additional step. If after computing a weighted least squares fit using carefully estimated weights, the residual plots still show the same funnel-shaped pattern as they did for the initial equally-weighted fit, it is likely that you may have forgotten to compute or plot the weighted residuals.
Example of WLS Using the Power Function Model The power function model for the weights, mentioned above, is often especially convenient when there is only one predictor variable. In this situation the general model given above can usually be simplified to the power function $$ \hat{\sigma}_i^2 \approx \gamma_1x_i^{\gamma_2} \, ,$$ which does not require the use of iterative fitting methods. This model will be used with the modified version of the Pressure/Temperature data, plotted below, to illustrate the steps needed to carry out a weighted least squares fit.
Modified Pressure/Temperature Data modified pressure/temperature data
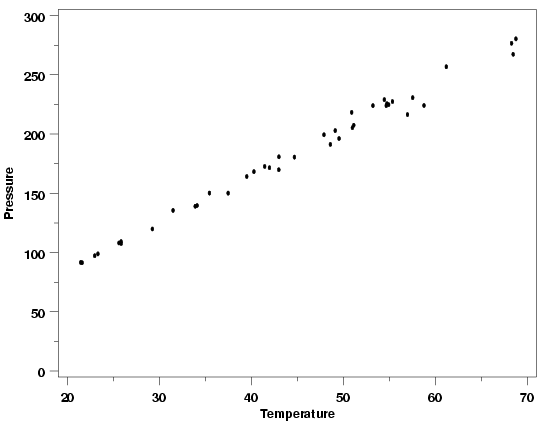
Defining Sets of Approximate Replicate Measurements From the data, plotted above, it is clear that there are not many true replicates in this data set. As a result, sets of approximate replicate measurements need to be defined in order to use the power function model to estimate the weights. In this case, this was done by rounding a multiple of the temperature to the nearest degree and then converting the rounded data back to the original scale. $$ \mbox{Temperature}_{\mbox{rep}} = 3 \cdot \mbox{round}(\mbox{Temperature}/3) $$ This is an easy way to identify sets of measurements that have temperatures that are relatively close together. If this process had produced too few sets of replicates, a smaller factor than three could have been used to spread the data out further before rounding. If fewer replicate sets were needed, then a larger factor could have been used. The appropriate value to use is a matter of judgment. An ideal value is one that doesn't combine values that are too different and that yields sets of replicates that aren't too different in size. A table showing the original data, the rounded temperatures that define the approximate replicates, and the replicate standard deviations is listed below.
Data with Approximate Replicates 
               Rounded              Standard
Temperature  Temperature  Pressure  Deviation
---------------------------------------------
   21.602        21        91.423    0.192333
   21.448        21        91.695    0.192333
   23.323        24        98.883    1.102380
   22.971        24        97.324    1.102380
   25.854        27       107.620    0.852080
   25.609        27       108.112    0.852080
   25.838        27       109.279    0.852080
   29.242        30       119.933   11.046422
   31.489        30       135.555   11.046422
   34.101        33       139.684    0.454670
   33.901        33       139.041    0.454670
   37.481        36       150.165    0.031820
   35.451        36       150.210    0.031820
   39.506        39       164.155    2.884289
   40.285        39       168.234    2.884289
   43.004        42       180.802    4.845772
   41.449        42       172.646    4.845772
   42.989        42       169.884    4.845772
   41.976        42       171.617    4.845772
   44.692        45       180.564          NA
   48.599        48       191.243    5.985219
   47.901        48       199.386    5.985219
   49.127        48       202.913    5.985219
   49.542        51       196.225    9.074554
   51.144        51       207.458    9.074554
   50.995        51       205.375    9.074554
   50.917        51       218.322    9.074554
   54.749        54       225.607    2.040637
   53.226        54       223.994    2.040637
   54.467        54       229.040    2.040637
   55.350        54       227.416    2.040637
   54.673        54       223.958    2.040637
   54.936        54       224.790    2.040637
   57.549        57       230.715   10.098899
   56.982        57       216.433   10.098899
   58.775        60       224.124   23.120270
   61.204        60       256.821   23.120270
   68.297        69       276.594    6.721043
   68.476        69       267.296    6.721043
   68.774        69       280.352    6.721043
The reader can download the modified Pressure/Temperature data as a text file.
Transformation of the Weight Data With the replicate groups defined, a plot of the ln of the replicate variances versus the ln of the temperature shows the transformed data for estimating the weights does appear to follow the power function model. This is because the ln-ln transformation linearizes the power function, as well as stabilizing the variation of the random errors and making their distribution approximately normal. $$ \begin{array}{ccl} \ln{(\hat{\sigma}_i^2)} & = & \ln{(\gamma_1x_i^{\gamma_2})} \\ & & \\ & = & \ln{(\gamma_1)} + \gamma_2\ln{(x_i}) \end{array} $$
Transformed Data for Weight Estimation with Fitted Model transformed data for weight estimation with fitted model
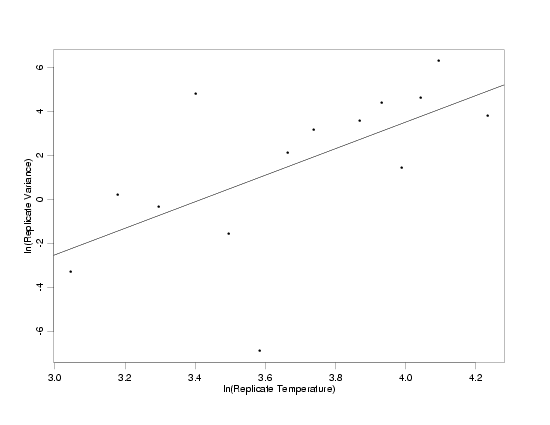
Specification of Weight Function The Splus output from the fit of the weight estimation model is shown below. Based on the output and the associated residual plots, the model of the weights seems reasonable, and $$ \begin{array}{ccl} w_{ij} & = & \mbox{Temperature}^{-\hat{\gamma}_2} \\ & & \\ & \approx & \mbox{Temperature}^{-6} \\ \end{array} $$ should be an appropriate weight function for the modified Pressure/Temperature data. The weight function is based only on the slope from the fit to the transformed weight data because the weights only need to be proportional to the replicate variances. As a result, we can ignore the estimate of \(\gamma_1\) in the power function since it is only a proportionality constant (in original units of the model). The exponent on the temperature in the weight function is usually rounded to the nearest digit or single decimal place for convenience, since that small change in the weight function will not affect the results of the final fit significantly.
Output from Weight Estimation Fit 
Residual Standard Error = 3.0245

Multiple R-Square = 0.3642

N = 14,  

F-statistic = 6.8744 on 1 and 12 df, p-value = 0.0223

                    coef std.err  t.stat p.value
Intercept       -20.5896  8.4994 -2.4225  0.0322
ln(Temperature)   6.0230  2.2972  2.6219  0.0223
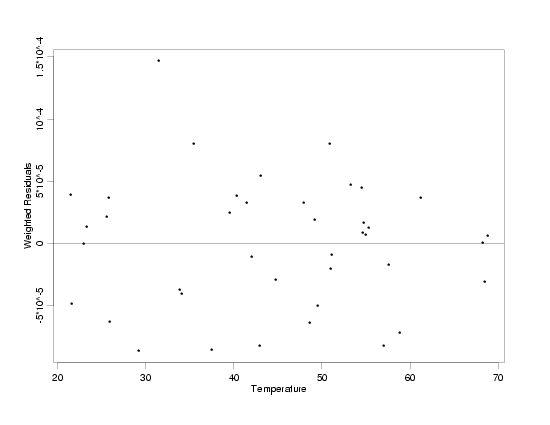
Fit of the WLS Model to the Pressure / Temperature Data With the weight function estimated, the fit of the model with weighted least squares produces the residual plot below. This plot, which shows the weighted residuals from the fit versus temperature, indicates that use of the estimated weight function has stabilized the increasing variation in pressure observed with increasing temperature. The plot of the data with the estimated regression function and additional residual plots using the weighted residuals confirm that the model fits the data well.
Weighted Residuals from WLS Fit of Pressure / Temperature Data weighted residuals from weighted least squares fit of pressure/temprerature data
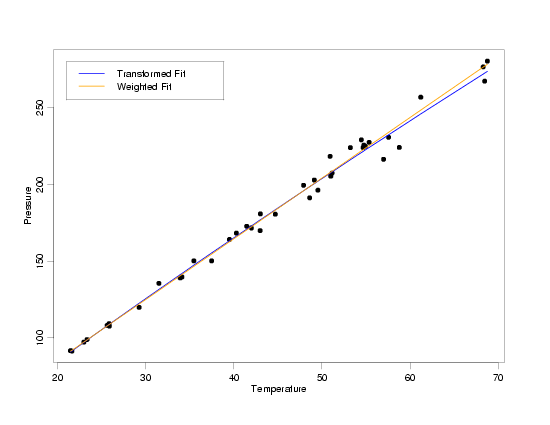
Comparison of Transformed and Weighted Results Having modeled the data using both transformed variables and weighted least squares to account for the non-constant standard deviations observed in pressure, it is interesting to compare the two resulting models. Logically, at least one of these two models cannot be correct (actually, probably neither one is exactly correct). With the random error inherent in the data, however, there is no way to tell which of the two models actually describes the relationship between pressure and temperature better. The fact that the two models lie right on top of one another over almost the entire range of the data tells us that. Even at the highest temperatures, where the models diverge slightly, both models match the small amount of data that is available reasonably well. The only way to differentiate between these models is to use additional scientific knowledge or collect a lot more data. The good news, though, is that the models should work equally well for predictions or calibrations based on these data, or for basic understanding of the relationship between temperature and pressure.
Home Tools & Aids Search Handbook Previous Page Next Page