4. Process Modeling
4.8. Some Useful Functions for Process Modeling
4.8.1. Univariate Functions
4.8.1.2. Rational Functions

4.8.1.2.5.

Quadratic / Quadratic Rational Function

Function:	${\displaystyle f(x)=\frac{{\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2}{1+{\beta }_{3}x+{\beta }_4{x}^2},{\beta }_2\ne 0,{\beta }_4\ne 0}$
Function Family:	Rational
Statistical Type:	Nonlinear
Domain:	${\displaystyle (-\mathrm{\infty },\mathrm{\infty })}$ with undefined points at ${\displaystyle x=\frac{-{\beta }_3\pm \sqrt{{\beta }_3^2-4{\beta }_4}}{2{\beta }_4}}$ There will be 0, 1, or 2 real solutions to this equation corresponding to whether ${\displaystyle {\beta }_3^2-4{\beta }_4}$ is negative, zero, or positive.
Range:	The range is complicated and depends on the specific values of ${\beta }_1,\dots ,{\beta }_5$.
Special Features:	Horizontal asymptotes at: ${\displaystyle y=\frac{{\beta }_2}{{\beta }_4}}$ and vertical asymptotes at: ${\displaystyle x=\frac{-{\beta }_3\pm \sqrt{{\beta }_3^2-4{\beta }_4}}{2{\beta }_4}}$ There will be 0, 1, or 2 real solutions to this equation corresponding to whether ${\displaystyle {\beta }_3^2-4{\beta }_4}$ is negative, zero, or positive.
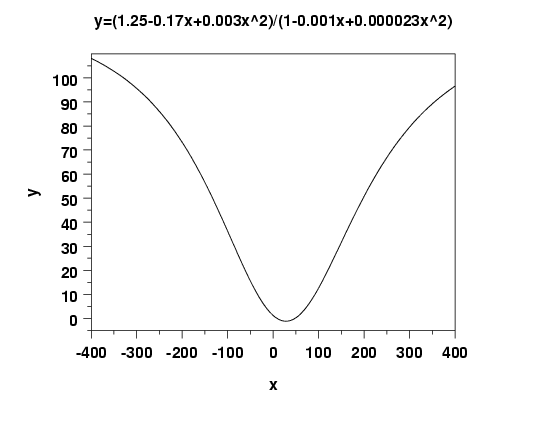
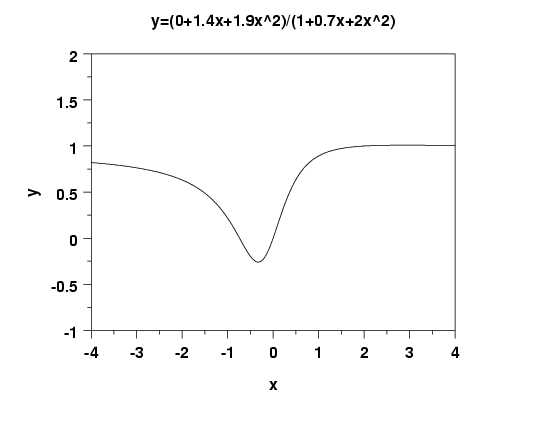
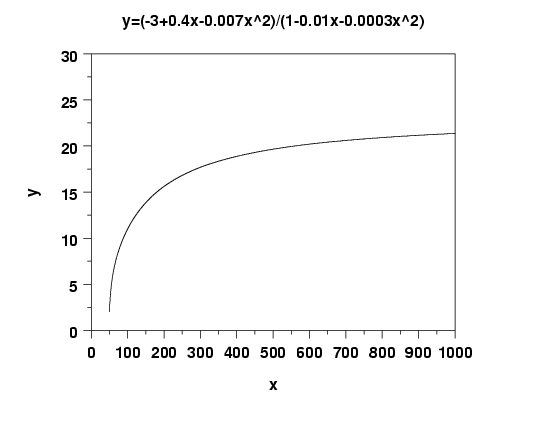
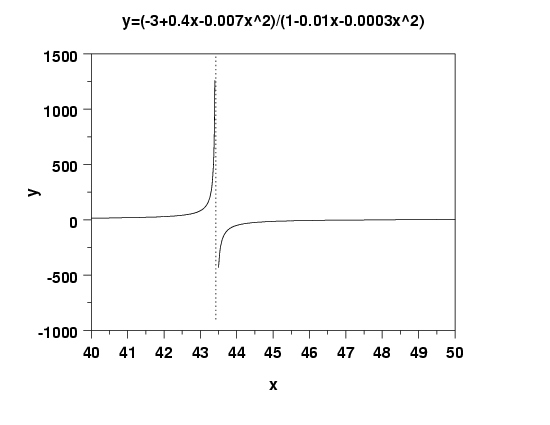
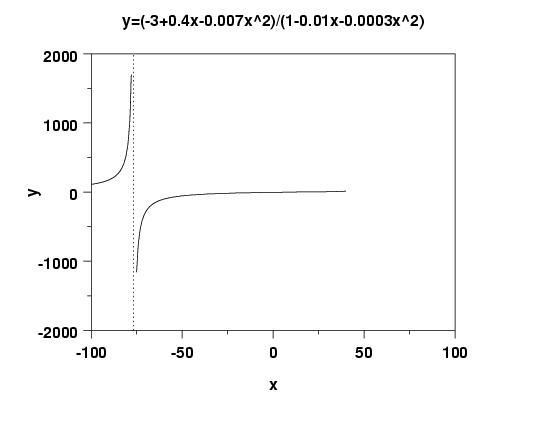
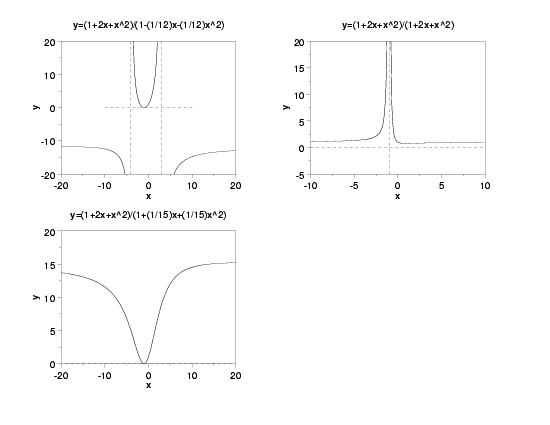
Additional Examples: