4.8.1.2.11. Determining m and n for Rational Function Models

4. Process Modeling
4.8. Some Useful Functions for Process Modeling
4.8.1. Univariate Functions
4.8.1.2. Rational Functions

4.8.1.2.11. Determining m and n for Rational Function Models

General Question

A general question for rational function models is:

I have data to which I wish to fit a rational function. What degrees $n$ and $m$ should I use for the numerator and denominator, respectively?

Four Questions

To answer the above broad question, the following four specific questions need to be answered.

What value should the function have at $x=\infty$? Specifically, is the value zero, a constant, or plus or minus infinity?
What slope should the function have at $x=\infty$? Specifically, is the derivative of the function zero, a constant, or plus or minus infinity?
How many times should the function equal zero (i.e., $f(x)=0$) for finite $x$?
How many times should the slope equal zero (i.e., $f'(x)=0$) for finite $x$?

These questions are answered by the analyst by inspection of the data and by theoretical considerations of the phenomenon under study.

Each of these questions is addressed separately below.

Question 1: What Value Should the Function Have at $x=\infty$?

Given the rational function, $$ R(x) = \frac{P_n(x)} {P_m(x)} $$ or $$ y = \frac{a_{n}x^{n} + a_{n-1}x^{n-1} + ... + a_{2}x^{2} + a_{1}x + a_{0}} {b_{m}x^{m} + b_{m-1}x^{m-1} + ... + b_{2}x^{2} + b_{1}x + b_{0}} \, , $$ then asymptotically, $$ R(x) \approx \left(\frac{a_n}{b_m}\right)x^{n-m} \, . $$ From this, it follows that:

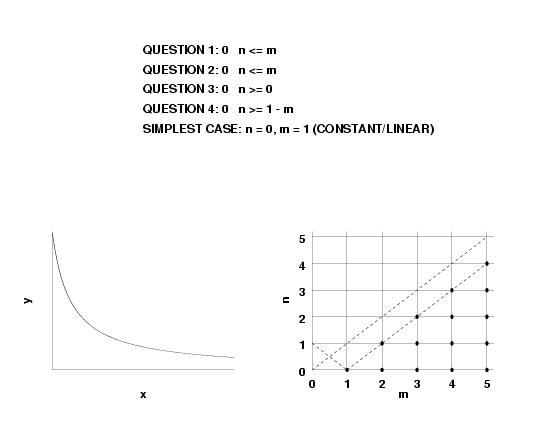
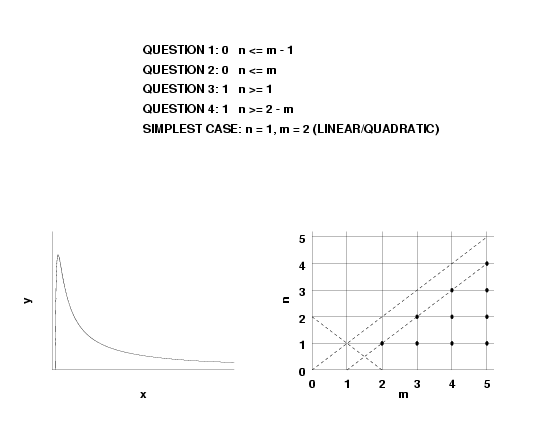
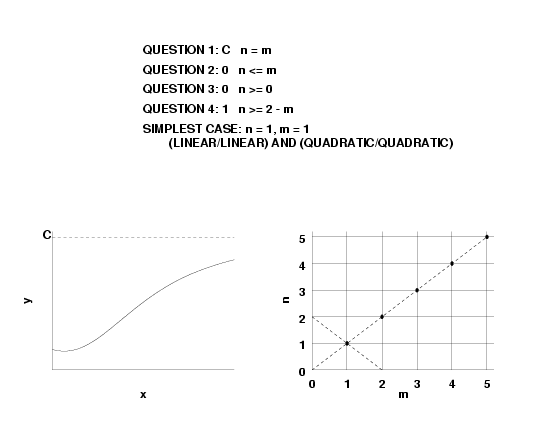
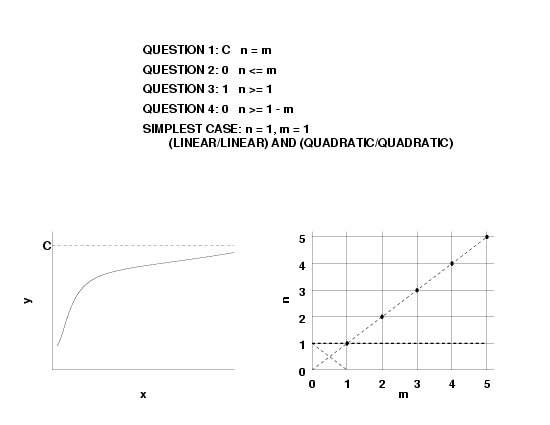
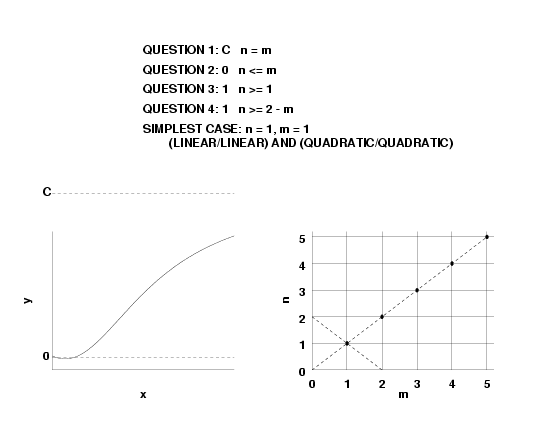
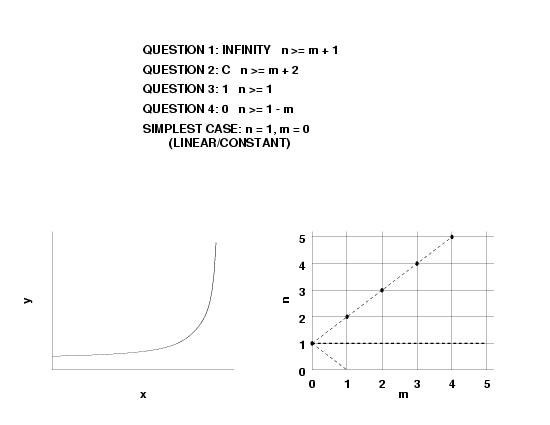
if $n \lt m, \, R(\infty)=0$,
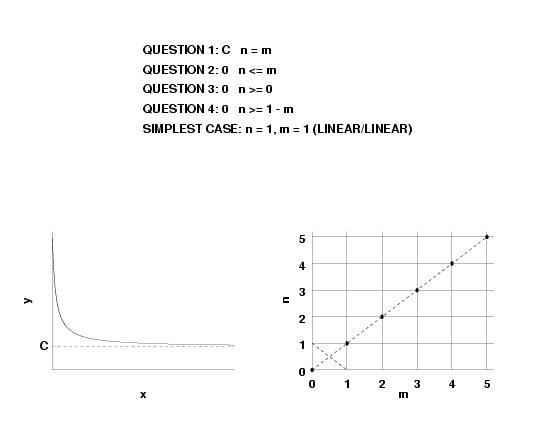
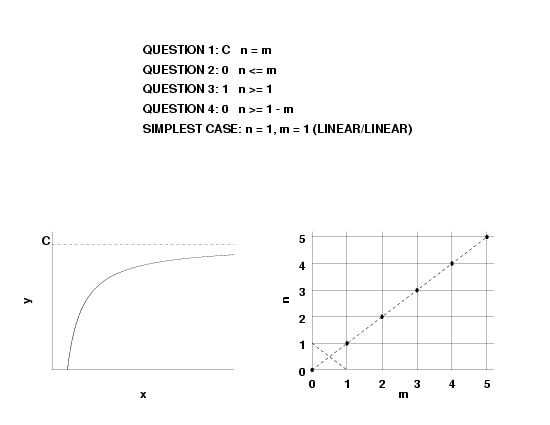
if $n = m, \, R(\infty) = a_n/b_m$, and
if $n \gt m, \, R(\infty) = \pm \infty$.

Conversely, if the fitted function, $f(x)$, is such that

$f(\infty) = 0$, this implies $n \lt m$.
$f(\infty) = constant$, this implies $n = m$.
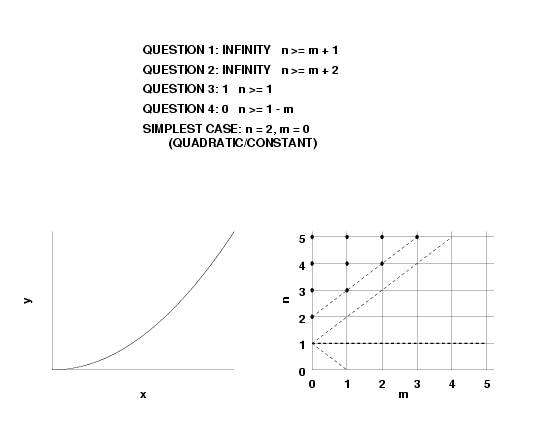
$f(\infty) = \pm \infty$, this implies $n \gt m$.

Question 2: What Slope Should the Function Have at $x=\infty$?

The slope is determined by the derivative of a function. The derivative of a rational function is $$ R'(x) = \frac{P_m(x)P'_n(x) - P_n(x)P'_m(x)} {[P_m(x)]^2} \, ,$$ with $$ \begin{eqnarray} P_n(x) &=& a_0 +a_1x + ... + a_nx^n \\ &=& \\ P'_n(x) &=& a_1 + 2a_2x + ... + na_nx^{n-1} \\ &=& \\ P_m(x) &=& b_0 + b_1x + ... + b_mx^m \\ &=& \\ P'_m(x) &=& b_1 + 2b_2x + ... + mb_mx^{m-1} \, .\\ \end{eqnarray} $$ Asymptotically, $$ R'(x) \approx (n - m)\left(\frac{a_n} {b_m}\right)x^{n-m-1} \, .$$ From this, it follows that

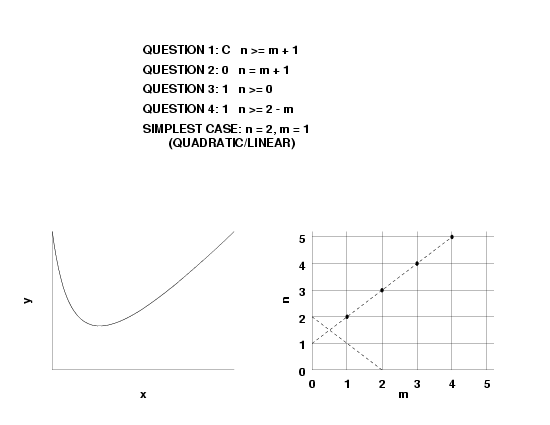
if $n < m, \, R'(\infty)=0$,
if $n = m, \, R'(\infty) = 0$,
if $n = m + 1, \, R'(\infty) = a_n/b_n$, and
if $n > m + 1, \, R'(\infty) = \pm \infty$.

Conversely, if the fitted function, $f(x)$, is such that

$f'(\infty)= 0$, this implies $n \le m$.
$f'(\infty) = constant$, this implies $n = m + 1$.
$f'(\infty) = \pm \infty$, this implies $ n > m + 1$.

Question 3: How Many Times Should the Function Equal Zero for Finite $x$?

For finite $x$, $R(x)=0$ only when the numerator polynomial, $P_n$, equals zero.

The numerator polynomial, and thus $R(x)$ as well, can have between zero and $n$ real roots. Thus, for a given $n$, the number of real roots of $R(x)$ is less than or equal to $n$.

Conversely, if the fitted function $f(x)$ is such that, for finite $x$, the number of times $f(x)=0$ is $k_3$, then $n$ is greater than or equal to $k_3$.

Question 4: How Many Times Should the Slope Equal Zero for Finite $x$?

The derivative function, $R'(x)$, of the rational function will equal zero when the numerator polynomial equals zero. The number of real roots of a polynomial is between zero and the degree of the polynomial.

For $n \ne m$, the numerator polynomial of $R'(x)$ has order $n + m - 1$. For $n = m$, the numerator polynomial of $R'(x)$ has order $n + m - 2$.

From this, it follows that

if $n \ne m$, the number of real roots of $R'(x), \, k_4, \, \mbox{ is } \le n + m - 1$.
if $n = m$, the number of real roots of $R'(x), \, k_4, \, \mbox{ is } \le n + m - 2$.

Conversely, if the fitted function $f(x)$ is such that, for finite $x$ and $n \ne m$ the number of times $f'(x) = 0$ is $k_4$, then $n + m - 1$ is $\ge k_4$. Similarly, if the fitted function $f(x)$ is such that, for finite $x$ and $n = m$, the number of times $f'(x) = 0$ is $k_4$, then $n + m - 2 \ge k_4$.

Tables for Determining Admissible Combinations of $m$ and $n$

In summary, we can determine the admissible combinations of $n$ and $m$ by using the following four tables to generate an $n$ versus $m$ graph. Choose the simplest ($n, m$) combination for the degrees of the intial rational function model.

1. Desired value of $f(\infty)$ Relation of $n$ to $m$

$0$
constant
$\infty$
$n \lt m$
$n = m $
$n \gt m $

2. Desired value of $f'(\infty)$ Relation of $n$ to $m$

$0$
constant
$\infty$
$n \lt m + 1$
$n = m + 1$
$n \gt m + 1$

3. For finite $x$, desired number, $k_3$, of times $f(x) = 0$ Relation of $n$ to $k_3$

$k_3$ $n \ge k_3$

4. For finite $x$, desired number, $k_4$, of times $f'(x) = 0$ Relation of $n$ to $k_4$ and $m$

$k_4 \, (n \ne m)$
$k_4 \, (n = m)$
$n \ge (1 + k_4)- m$
$n \ge (2 + k_4) - m$

Examples for Determing $m$ and $n$

The goal is to go from a sample data set to a specific rational function. The graphs below summarize some common shapes that rational functions can have and shows the admissible values and the simplest case for $n$ and $m$. We typically start with the simplest case. If the model validation indicates an inadequate model, we then try other rational functions in the admissible region.

Shape 1

Shape 2

Shape 3

Shape 4

Shape 5

Shape 6

Shape 7

Shape 8

Shape 9

Shape 10