3.
Production
Process Characterization
3.1.
Introduction to Production Process
Characterization
3.1.3.
Terminology/Concepts
3.1.3.2.
|
Process Variability
|
|
|
Variability is present everywhere
|
All manufacturing and measurement processes exhibit
variation. For example, when we take sample data on the output of a process,
such as critical dimensions, oxide thickness, or resistivity, we observe
that all the values are NOT the same. This results in a collection
of observed values distributed about some location value. This is what
we call spread or variability. We represent variability numerically with
the variance calculation
and graphically with a
histogram.
|
|
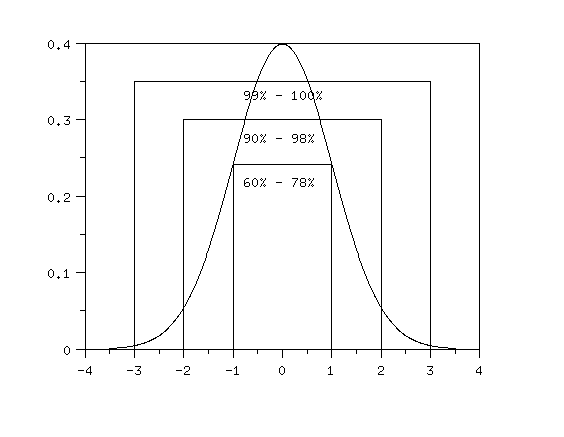
How does the standard deviation describe the spread of the data?
|
The standard deviation (square root of the variance)
gives insight into the spread of the data through the use of what is known
as the Empirical Rule. This rule (shown in the graph below) is:
Approximately 60-78% of the data are within a distance of one standard
deviation from the average
\( (\bar{x} - s, \bar{x} + s) \).
Approximately 90-98% of the data are within a distance of two standard
deviations from the average
\( (\bar{x} - 2s, \bar{x} + 2s) \).
More than 99% of the data are within a distance of three standard
deviations from the average
\( (\bar{x} - 3s, \bar{x} + 3s) \).
|
|
|
|
|
Variability accumulates from many sources
|
This observed variability is an accumulation of many different sources of
variation that have occurred throughout the manufacturing process. One
of the more important activities of process characterization is to
identify and quantify these various sources of variation so that they may
be minimized.
|
|
There are also different types
|
There are not only different sources of variation, but there are also
different types of variation. Two important classifications
of variation for the purposes of PPC are controlled variation and
uncontrolled variation.
|
|
Click here to see examples
|
-
CONTROLLED VARIATION
-
Variation that is characterized by a stable and consistent pattern
of variation over time. This type of variation will be random in
nature and will be exhibited by a uniform fluctuation about a constant
level.
-
UNCONTROLLED VARIATION
-
Variation that is characterized by a pattern of variation that
changes over time and hence is unpredictable. This type of
variation will typically contain some structure.
|
|
Stable processes only exhibit controlled variation
|
This concept of controlled/uncontrolled variation is important
in determining if a process is stable. A process is deemed stable
if it runs in a consistent and predictable manner. This means that the
average process value is constant and the variability is controlled. If
the variation is uncontrolled, then either the process average is changing
or the process variation is changing or both. The first process in the
example above is stable; the second is not.
|
|
In the course of process characterization we should endeavor
to eliminate all sources of uncontrolled variation.
|


