7. Product and Process Comparisons
7.4. Comparisons based on data from more than two processes
7.4.2. Are the means equal?

7.4.2.1.

1-Way ANOVA overview

An overview of the one-way ANOVA is given in this section
 
 
 
 
 
 
 
 
 
 

What are sums of squares and degrees of freedom?
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 The guiding principle behind ANOVA is the decomposition of the sums of squares, or Total SS 
 
 
 
 
 
 
 
 
 
 
 

Definition of "Treatment"
 

First we explain the principals involved in the 1-way ANOVA. 

In an analysis of variance the variation in the response measurements is partitoned into components that correspond to different sources of variation.

The goal in this procedure is to split the total variation in the data into a portion due to random error and portions due to changes in the values of the independent variable(s). 

The variance of n measurements is given by 

The numerator part is called the sum of squares of deviations from the mean, and the denominator is called the degrees of freedom. 

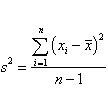
The variance, after some algebra, can be rewritten as: 

The first term in the numerator  is called the "raw sum of squares" and the second term is called the "correction term for the mean"  Another name for the numerator is the "corrected sum of squares", and this is usually abbreviated by Total SS. 

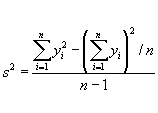
The SS in a 1-way ANOVA can be split up into two components, called the "sum of squares of treatments" and "sum of squares of error", abbreviated as SST and SSE. 

Algebraically, this is expressed by 

where k is the number of treatments and the bar over the x.. denotes the "grand" or "overall" mean. Each n_i is the number  of observations for treatment i. The total number of observations is N (the sum of the n_i).

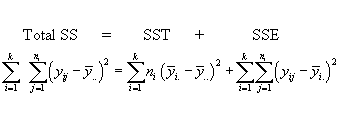
Don't be alarmed by the double subscripting. The total SS can be written single or double subscripted. The double subscript stems from the way the data are arranged in the data table. The table is usually a rectangular array with k columns and each column consists of n_i rows (however, the lengths of the rows, or the n_i, may be unequal).

We introduced the concepts of treatment.  The definition is: A treatment is a specific combination of factor levels whose effect is to be compared with other treatments.