7. Product and Process Comparisons
7.4. Comparisons based on data from more than two processes
7.4.2. Are the means equal?

7.4.2.7.

The two-way ANOVA

The 2-way ANOVA is probably the most popular layout in Design of Experiments
 
 
 
 
 
 

The breakdown of the total (corrected for the mean) sums of squares
 
 
 

 

To begin with, let us define a factorial experiment: 

An experiment that utilizes every combination of factor levels as treatments is called a factorial experiment.

In a factorial experiment with factor A at a levels and factor B at b levels, the model for the general layout can be written as 

where m is the overall mean response, t_i is the effect due to the i-th level of factor A, b_j is the effect due to the j-th level of factor B and g_ij is the effect due to any interaction between the i-th level of A and the j-th level of B.

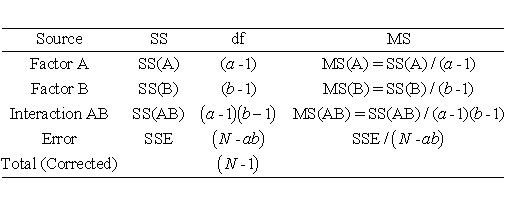
When an  a x b  factorial experiment is conducted with an equal number of observation per treatment combination, the total (corrected) sum of squares is partitioned as: 

               SStotal = SS(A) + SS(B) + SS(AB) + SSE

where AB represents the interaction between A and B.

The resulting ANOVA table for an a x b factorial experiment is