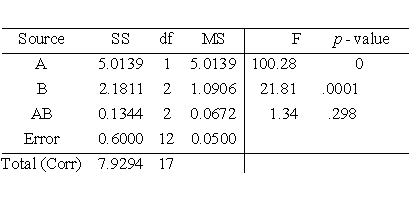
7.4. Comparisons based on data from more than two processes
7.4.2. Are the means equal?
7.4.2.8. |
Models and calculations for the two-way ANOVA |
How to obtain sums of squares for the balanced factorial layout
2-way ANOVA Example
Factor A has 1, 2, ..., a levels. Factor B has 1, 2, ..., b levels. There are ab treatment combinations (or cells) in a complete factorial layout. Assume that each treatment cell has r independent obsevations (known as replications). When each cell has the same number of replications, the design is balanced factorial. In this case, the abr data points {yijk}can be shown pictorially as follows:
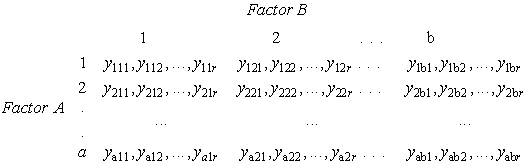
Next, we will calculate the sums of squares needed for the ANOVA table.
Let Ai be the sum of all observations of level i of factor A, i = 1, ... ,a. The Ai are the row sums.
Let Bj be the sum of all observations of level j of factor B, j = 1, ...,b. The Bj are the column sums.
Let (AB)ij be the sum of all observations of level i of A and level j of B. These are cell sums.
Let r be the number of replicates in the experiment, that is: the number of times each factorial treatment combination appears in the experiment.
Then the total number of observations for each level of factor A is rb and the total number of observations for each level of factor B is ra and the total number of observations for each interaction is r.
Finally, the total number of observations n in the experiment is abr.
With the help of these expressions we arrive (omitting derivations) at
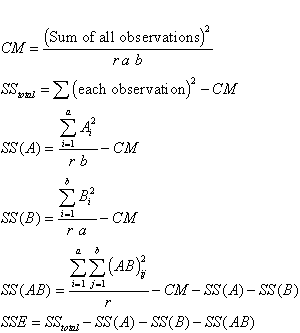
These expressions are used to calculate the ANOVA table entries for the (fixed effects) 2-way ANOVA.
Example:
An evaluation of a new coating applied to 3 different materials was conducted at 2 different laboratories. Each laboratory tested 3 samples from each of the treated materials. The results are given in the next table:
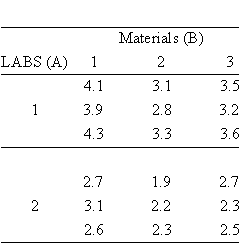
The preliminary part of the analysis yields a table of row and column
sums

From this table we generate the ANOVA table.