7.
Product and Process Comparisons
7.4.
Comparisons based on data from more than two processes
7.4.3.
Are the means equal?
7.4.3.6.
|
Assessing the response from any factor combination
|
|
|
Contrasts
|
This page treats how to estimate and put confidence bounds
around the response to different combinations of factors. Primary
focus is on the combinations that are known as
contrasts.
We begin, however, with the simple case of a single factor-level
mean.
|
|
|
Estimation of a Factor Level Mean With Confidence Bounds
|
|
Estimating factor level means
|
An unbiased estimator of the factor level mean \(\mu_i\)
in the one-way ANOVA model is given by:
$$ \hat{\mu}_i = \bar{Y}_{i \huge{\cdot}} \, , $$
where
$$ \bar{Y}_{i \huge{\cdot}} = \frac{\sum_{j=1}^{n_i} Y_{ij}}{n_i} = \frac{Y_{i \huge{\cdot}}}{n_i} \, . $$
|
|
Variance of the factor level means
|
The variance of this sample mean estimator is
$$ s_{\bar{Y}_{i \huge{\cdot}}}^2 = \frac{MSE}{n_i} = \frac{\hat{\sigma}_e^2}{n_i} \, . $$
|
|
Confidence intervals for the factor level means
|
It can be shown that:
$$ t = \frac{\bar{Y}_{i \huge{\cdot}} - \mu_i}{s_{\bar{Y}_{i \huge{\cdot}}}} \, , $$
has a \(t\)
distribution with \((N-k)\)
degrees of freedom for the ANOVA model under consideration, where \(N\)
is the total number of observations and \(k\)
is the number of
factor levels or groups. The degrees of freedom are the same as
were used to calculate the MSE in the ANOVA table. That is:
dfe (degrees of freedom for error) = \(N - k\).
From this we can calculate\(100(1-\alpha)\) %
confidence limits for each \(\mu_i\).
These are given by:
$$ \bar{Y}_{i\cdot} \pm t_{1-\alpha/2, \, N-k} \,\,\sqrt{\frac{\hat{\sigma}^2_\epsilon}{n_i}} \, . $$
|
|
|
Example 1
|
|
Example for a 4-level treatment (or 4 different treatments)
|
The data in the accompanying table resulted from an experiment run in
a completely randomized design in which each of four treatments was
replicated five times.
|
|
|
|
|
|
Total |
Mean |
|
| Group 1 |
6.9 |
5.4 |
5.8 |
4.6 |
4.0 |
26.70 |
5.34 |
| Group 2 |
8.3 |
6.8 |
7.8 |
9.2 |
6.5 |
38.60 |
7.72 |
| Group 3 |
8.0 |
10.5 |
8.1 |
6.9 |
9.3 |
42.80 |
8.56 |
| Group 4 |
5.8 |
3.8 |
6.1 |
5.6 |
6.2 |
27.50 |
5.50 |
|
| All Groups |
|
|
|
|
135.60 |
6.78 |
|
|
One-way ANOVA table layout
|
This experiment can be illustrated by the table layout for this one-way
ANOVA experiment shown below:
|
Level
|
|
|
Sample j
|
|
|
|
|
|
i
|
1
|
2
|
...
|
5
|
Sum
|
Mean
|
N
|
|
|
1
|
Y11
|
Y12
|
...
|
Y15
|
Y1.
|
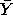 1. 1.
|
n1
|
|
2
|
Y21
|
Y22
|
...
|
Y25
|
Y2.
|
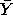 2. 2.
|
n2
|
|
3
|
Y31
|
Y32
|
...
|
Y35
|
Y3.
|
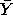 3. 3.
|
n3
|
|
4
|
Y41
|
Y42
|
...
|
Y45
|
Y4.
|
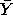 4. 4.
|
n4
|
|
|
All
|
|
|
|
|
Y.
|
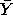 .. ..
|
nt
|
|
|
ANOVA table
|
The resulting ANOVA table is
|
Source
|
SS
|
DF
|
MS
|
F
|
|
Treatments
|
38.820
|
3
|
12.940
|
9.724
|
|
Error
|
21.292
|
16
|
1.331
|
|
|
Total (Corrected)
|
60.112
|
19
|
|
|
|
|
Mean
|
919.368
|
1
|
|
|
|
Total (Raw)
|
979.480
|
20
|
|
|
The estimate for the mean of group 1 is 5.34, and the sample size
is \(n_1\)
= 5.
|
|
Computing the confidence interval
|
Since the confidence interval is two-sided, the entry \((1-\alpha/2)\)
value for the \(t\)
table is (1 - 0.05/2) = 0.975, and the
associated degrees of freedom is \(N\)
- 4, or 20 - 4 = 16.
From the t table
in Chapter 1, we obtain \(t_{0.975, \, 16}\)
= 2.120.
Next we need the standard error of the mean for group 1:
$$ s_{\bar{Y}_{1 \huge{\cdot}}}^2 = \frac{MSE}{n_1} = \frac{1.331}{5} = 0.2662 $$
$$ s_{\bar{Y}_{1 \huge{\cdot}}} = \sqrt{0.2662} = 0.5159 \, . $$
Hence, we obtain confidence limits 5.34 ± 2.120 (0.5159) and
the confidence interval is
$$ 4.246 \le \mu_1 \le 6.434 \, . $$
|
|
|
Definition and Estimation
of Contrasts
|
|
Definition of contrasts and orthogonal contrasts
|
Definitions
A contrast is a linear combination of two or more factor level means
with coefficients that sum to zero.
Two contrasts are orthogonal if the sum of the products of
corresponding coefficients (i.e., coefficients for the same means)
adds to zero.
Formally, the definition of a contrast is expressed below, using the
notation \(\mu_i\)
for the \(i\)-th
treatment mean:
$$ C = c_1 \mu_1 + c_2 \mu_2 + \cdots + c_j \mu_j + \cdots + c_k \mu_k \, , $$
where
$$ c_1 + c_2 + \cdots + c_j + \cdots + c_k = \sum_{j=1}^k c_j = 0 \, . $$
Simple contrasts include the case of the difference between two
factor means, such as \(\mu_1 - \mu_2\).
If one wishes to compare treatments 1 and 2 with treatment 3, one
way of expressing this is by: \(\mu_1 + \mu_2 - 2\mu_3\).
Note that
\(\mu_1 - \mu_2\)
has coefficients +1, -1.
\(\mu_1 + \mu_2 - 2\mu_3\)
has coefficients +1, +1, -2.
These coefficients sum to zero.
|
|
An example of orthogonal contrasts
|
As an example of orthogonal contrasts, note the three
contrasts defined by the table below, where the rows denote
coefficients for the column treatment means.
|
|
|
\(\mu_1\)
|
\(\mu_2\)
|
\(\mu_3\)
|
\(\mu_4\)
|
|
| \(c_1\)
|
+1
|
0
|
0
|
-1
|
| \(c_2\)
|
0
|
+1
|
-1
|
0
|
| \(c_3\)
|
+1
|
-1
|
-1
|
+1
|
|
|
|
Some properties of orthogonal contrasts
|
The following is true:
- The sum of the coefficients for each contrast is zero.
- The sum of the products of coefficients of each pair of
contrasts is also 0 (orthogonality property).
- The first two contrasts are simply pairwise comparisons,
the third one involves all the treatments.
|
|
Estimation of contrasts
|
As might be expected, contrasts are estimated by taking the
same linear combination of treatment mean estimators. In other
words:
$$ \hat{C} = \sum_{i=1}^r c_i \bar{Y}_{i \huge{\cdot}} $$
and
$$ \mbox{Var } (\hat{C}) = \sum_{i=1}^r c_i^2 \cdot \mbox{ Var } (\bar{Y}_{i \huge{\cdot}}) =
\sum_{i=1}^r c_i^2 \left( \frac{\sigma^2}{n_i} \right) = \sigma^2 \sum_{i=1}^r \frac{c_i^2}{n_i} \, . $$
Note: These formulas hold for any linear combination of
treatment means, not just for contrasts.
|
|
|
Confidence Interval for a Contrast
|
|
Confidence intervals for contrasts
|
An unbiased estimator for a contrast \(C\)
is given by
$$ \hat{C} = \sum_{i=1}^r c_i \bar{Y}_{i \huge{\cdot}} \, . $$
The estimator of \(\mbox{Var }(\hat{C})\)
is
$$ s_{\hat{C}}^2 = \hat{\sigma}_e^2 \, \sum_{i=1}^r \frac{c_i^2}{n_i} \, . $$
The estimator \(\hat{C}\)
is normally distributed because it is a linear
combination of independent normal random variables. It can be
shown that:
$$ \frac{\hat{C} - C}{s_{\hat{C}}} \, , $$
is distributed as \(t_{N-r}\)
for the one-way ANOVA model under discussion.
Therefore, the \(1-\alpha\)
confidence limits for \(C\)
are:
$$ \hat{C} \pm t_{1-\alpha/2, \, N-r} \,\, s_{\hat{C}} \, . $$
|
|
|
Example 2 (estimating contrast)
|
|
Contrast to estimate
|
We wish to estimate, in our previous example, the following contrast:
$$ C = \frac{\mu_1 + \mu_2}{2} - \frac{\mu_3 + \mu_4}{2} \, , $$
and construct a 95 % confidence interval for \(C\).
|
|
Computing the point estimate and standard error
|
The point estimate is:
$$ \hat{C} = \frac{\bar{Y}_1 + \bar{Y}_2}{2} - \frac{\bar{Y}_3 + \bar{Y}_4}{2} = -0.5 \, . $$
Applying the formulas above we obtain
$$ \sum_{i=1}^4 \frac{c_i^2}{n_i} = \frac{4(1/2)^2}{5} = 0.2 $$
and
$$ s_{\hat{C}}^2 = MSE \, \sum_{i=1}^4 \frac{c_i^2}{n_i} = 1.331(0.2) = 0.2662 \, , $$
and the standard error is \(\sqrt{0.2661} = 0.5159\).
|
|
Confidence interval
|
For a confidence coefficient of 95 % and df = 20 - 4 = 16,
\(t_{0.975, \, 16}\)
= 2.12. Therefore, the desired 95 %
confidence interval is -0.5 ± 2.12(0.5159) or
(-1.594, 0.594).
|
|
|
Estimation of Linear Combinations
|
|
Estimating linear combinations
|
Sometimes we are interested in a linear combination of the
factor-level means that is not a contrast. Assume that in our
sample experiment certain costs are associated with each group.
For example, there might be costs associated with each factor as
follows:
|
Factor
|
Cost in $
|
|
1
|
3
|
|
2
|
5
|
|
3
|
2
|
|
4
|
1
|
The following linear combination might then be of interest:
$$ C = 3\mu_1 + 5\mu_2 + 2\mu_3 + 1\mu_4 \, . $$
|
|
Coefficients do not have to sum to zero for linear combinations
|
This resembles a contrast, but the coefficients \(c_i\)
do not sum to zero. A linear combination is given by the definition:
$$ C = \sum_{i=1}^r c_i \mu_i \, , $$
with no restrictions on the coefficients \(c_i\).
|
|
Confidence interval identical to contrast
|
Confidence limits for a linear combination \(C\)
are obtained in
precisely the same way as those for a contrast, using the same
calculation for the point estimator and estimated variance.
|
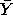 1.
1.
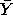 2.
2.
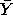 3.
3.
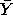 4.
4.
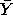 ..
..

