7. Product and Process Comparisons
7.4. Comparisons based on data from more than two processes
7.4.6. How can we make multiple comparisons?

7.4.6.4.

Comparing multiple proportions: The Marascuillo procedure

 
 
 
 
 
 
 
 

A procedure to simultaneously test the differences of all pairs of  proportions when there are several populations under investigation
 
 
 

The test criteria for the absolute value of the difference of a pair of proportions
 
 
 
 

Example 

 

Earlier, we discussed how to test whether several populations have the same proportion of defects. The example given there led to rejection of the null hypothesis of equality. 

Rejecting the null hypothesis only allows us to conclude that not (in this case) all lots are equal with respect to the proportion of defectives. However, It does not tell us which lot or lots caused the rejection. 
The Marascuilo procedure enables us to simultaneously compare all possible pairs of proportions. 

The Marascuillo Procedure

Assume we have samples of size n_i (i = 1, 2, ..., k) from k populations. The first step of this procedure is to compute the differences p_i - p_j , (where i is not equal to j) among all k(k-1)/2 pairs of proportions. 

The absolute values of these differences are the test-statistics. 

Step 2 is to pick a significance level and compute the the corresponding critical values for the Marascuilo procedure from 

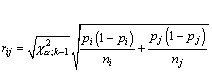
The third and last step is to compare each of the k(k-1)/2  test statistics against its corresponding critical r_ij value. Those pairs that have a test statistic that exceeds the critical value are significant at the a level. 

Example

To illustrate the Marascuillo procedure we use the data from the previous example. Since there were 5 lots, there are (5 x 4)/2 = 10 possible pairwise comparisons to be made and ten critical ranges to compute. The five sample proportions are: 

                             p₁ =  36/300  = .120 
                             p₂ =  46/300  = .150 
                             p₃ =  42/300  = .140 
                             p₄ =  63/300  = .210 
                             p₅ =  38/300  = .127 

For an overall level of significance of .05, the upper-tailed critical value of the chi-square distribution having four degrees of freedom is 11.143 and the square root of 11.143 is 3.338.  Calculating the 10 absolute differences and the 10 critical values leads to the following summary table. 

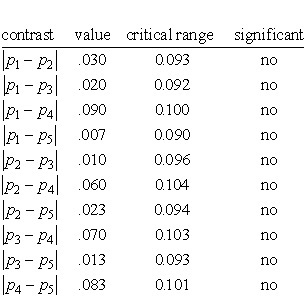
A difference is statistically significant if its value exceeds the critical range value. In this example, even though the null hypothesis of equality was rejected earlier, there is not enough data to conclude any particular difference is significant. Note, however,  that all the comparisons involving population 4 come the closest to significance - leading us to suspect that more data might actually show that population 4 does have a significantly higher proportion of defects.