5. Process Improvement
5.3. Choosing an experimental design
5.3.3. How do you select an experimental design?
5.3.3.4. Fractional factorial designs

5.3.3.4.1.

A 23-1 design (half of a 23)

We can run a fraction of a full factorial experiment and still be able to estimate main effects

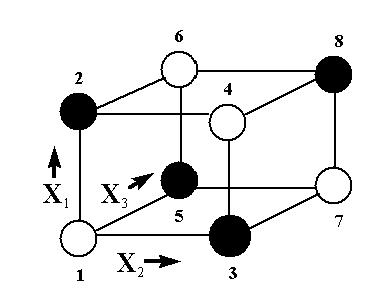
Consider the two-level, full factorial design for three factors, namely the 2³ design. This implies eight runs (not counting replications or center points). Graphically, as shown earlier, we can represent the 2³ design by the following cube:

FIGURE 3.4: A 2³ Full Factorial Design;
Factors X₁, X₂, X₃. (The arrows show the direction of increase of the factors. Numbers `1' through '8' at the corners of the design cube reference the 'Standard Order' of runs)

Tabular representation of the design

In tabular form, this design (also showing eight observations 'y_j' (j = 1,...,8) is given by

TABLE 3.11: A 2³ Two-level, Full Factorial Design Table Showing Runs in 'Standard Order,' Plus Observations (y_j)

	X1	X2	X3	Y
1	-1	-1	-1	y1 = 33
2	+1	-1	-1	y2 = 63
3	-1	+1	-1	y3 = 41
4	+1	+1	-1	Y4 = 57
5	-1	-1	+1	y5 = 57
6	+1	-1	+1	y6 = 51
7	-1	+1	+1	y7 = 59
8	+1	+1	+1	y8 = 53

Responses in standard order

The right-most column of the table lists 'y₁' through 'y₈' to indicate the responses measured for the experimental runs when listed in standard order. For example, `y₁' is the response (i.e., output) observed when the three factors were all run at their 'low' setting. The numbers entered in the 'y' column will be used to illustrate calculations of effects.

Computing X₁ main effect

From the entries in the table we are able to compute all 'effects' such as main effects, first-order 'interaction' effects, etc. For example, to compute the main effect estimate 'c₁' of factor X₁, we compute the average response at all runs with X₁ at the 'high' setting, namely (1/4)(y₂ + y₄ + y₆ + y₈), minus the average response of all runs with X₁ set at 'low,' namely (1/4)(y₁ + y₃ + y₅ + y₇). That is,

c1	=	(1/4) (y2 + y4 + y6 + y8) - (1/4) (y1 + y3 + y5 + y7)
	=	(1/4) (63+57+51+53 ) - (1/4) (33+41+57+59)
	=	8.5

Can we estimate X1 main effect with four runs?

Suppose, however, that we only have enough resources to do four runs. Is it still possible to estimate the main effect for X₁? Or any other main effect? The answer is yes, and there are even different choices of the four runs that will accomplish this.

Example of computing the main effects using only four runs

For example, suppose we select only the four light (unshaded) corners of the design cube. Using these four runs (1, 4, 6 and 7), we can still compute c₁ as follows:

c1	=	(1/2) (y4 + y6) - (1/2) (y1 + y7)
	=	(1/2) (57+51) - (1/2) (33+59)
	=	8

Simarly, we would compute c₂, the effect due to X₂, as

c2	=	(1/2) (y4 + y7) - (1/2) (y1 + y6)
	=	(1/2) (57+59) - (1/2) (33+51)
	=	16

Finally, the computation of c₃ for the effect due to X₃ would be

c3	=	(1/2) (y6 + y7) - (1/2) (y1 + y4)
	=	(1/2) (51+59) - (1/2) (33+57)
	=	10

Alternative runs for computing main effects

We could also have used the four dark (shaded) corners of the design cube for our runs and obtained similiar, but slightly different, estimates for the main effects. In either case, we would have used half the number of runs that the full factorial requires. The half fraction we used is a new design written as 2^3-1. Note that 2^3-1 = 2³/2 = 2² = 4, which is the number of runs in this half-fraction design. In the next section, a general method for choosing fractions that "work" will be discussed.

Example of how fractional factorial experiments often arise in industry

Example: An engineering experiment calls for running three factors, namely Pressure, Table speed, and Down force, each at a 'high' and a 'low' setting, on a production tool to determine which has the greatest effect on product uniformity. Interaction effects are considered negligible, but uniformity measurement error requires that at least two separate runs (replications) be made at each process setting. In addition, several 'standard setting' runs (centerpoint runs) need to be made at regular intervals during the experiment to monitor for process drift. As experimental time and material are limited, no more than 15 runs can be planned.

A full factorial 2³ design, replicated twice, calls for 8x2 = 16 runs, even without centerpoint runs, so this is not an option. However a 2^3-1 design replicated twice requires only 4x2 = 8 runs, and then we would have 15-8 = 7 spare runs: 3 to 5 of these spare runs can be used for centerpoint runs and the rest saved for backup in case something goes wrong with any run. As long as we are confident that the interactions are negligbly small (compared to the main effects), and as long as complete replication is required, then the above replicated 2^3-1 fractional factorial design (with center points) is a very reasonable choice.

On the other hand, if interactions are potentially large (and if the replication required could be set aside), then the usual 2³ full factorial design (with center points) would serve as a good design.