5.
Process Improvement
5.3.
Choosing an experimental design
5.3.3.
How do you select an experimental design?
5.3.3.6.
Response surface designs
5.3.3.6.1.
|
Central Composite Designs (CCD)
|
|
|
|
Box-Wilson Central Composite Designs
|
|
CCD designs start with a factorial or fractional factorial design
(with center points) and add "star" points to estimate curvature
|
A Box-Wilson Central Composite Design, commonly called 'a central
composite design,' contains an imbedded factorial or fractional
factorial design with center points that is augmented with a group of
'star points' that allow estimation of curvature. If the distance from
the center of the design space to a factorial point is ±1 unit
for each factor, the distance from the center of the design space to a
star point is
|\( \alpha \)| > 1. The precise value of
\( \alpha \) depends on certain properties desired for the design and on
the number of factors involved.
Similarly, the number of centerpoint runs the design is to contain also
depends on certain properties required for the design.
|
|
Diagram of central composite design generation for two factors
|
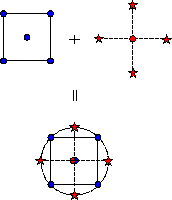
FIGURE 3.20: Generation of a Central Composite Design for Two
Factors
|
|
A CCD design with k factors has 2k star points
|
A central composite design always contains twice as many star points
as there are factors in the design. The star points represent new
extreme values (low and high) for each factor in the design. Table
3.22 summarizes the properties of the three varieties of central
composite designs. Figure 3.21 illustrates the relationships among
these varieties.
|
|
Description of 3 types of CCD designs, which depend on where the
star points are placed
|
TABLE 3.22: Central Composite Designs
Central Composite
Design Type
|
Terminology
|
Comments
|
|
Circumscribed
|
CCC
|
CCC designs are the original form of the central composite design.
The star points are at some distance
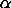 from
the center based on the properties desired for the design and the number
of factors in the design. The star points establish new extremes
for the low and high settings for all factors. Figure 5 illustrates
a CCC design. These designs have circular, spherical, or hyperspherical
symmetry and require 5 levels for each factor. Augmenting an existing
factorial or resolution V fractional factorial design with star points
can produce this design.
|
|
Inscribed
|
CCI
|
For those situations in which the limits specified for factor settings
are truly limits, the CCI design uses the factor settings as the star
points and creates a factorial or fractional factorial design within
those limits (in other words, a CCI design is a scaled down CCC design
with each factor level of the CCC design divided by
\( \alpha \) to generate the CCI design). This design also requires
5 levels of each factor.
|
|
Face Centered
|
CCF
|
In this design the star points are at the center of each face of the
factorial space, so
\( \alpha \) = ± 1. This variety requires 3 levels of each factor.
Augmenting an existing factorial or resolution V design with appropriate
star points can also produce this design.
|
|
|
Pictorial representation of where the star points are placed for
the 3 types of CCD designs
|
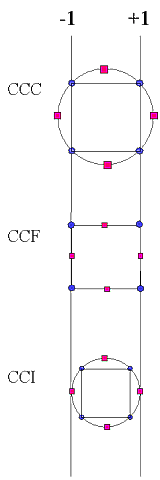
FIGURE 3.21: Comparison of the Three Types of Central
Composite Designs
|
|
Comparison of the 3 central composite designs
|
The diagrams in Figure 3.21 illustrate the three types of central
composite designs for two factors. Note that the CCC explores the
largest process space and the CCI explores the smallest process space.
Both the CCC and CCI are
rotatable designs,
but the CCF is not. In the CCC design, the design points describe
a circle circumscribed about the factorial square. For three
factors, the CCC design points describe a sphere around the factorial
cube.
|
|
|
Determining
\( \alpha \) in Central Composite Designs
|
|
The value of
\( \alpha \) is chosen to maintain rotatability
|
To maintain rotatability, the value of
\( \alpha \) depends on the number of experimental runs in the factorial
portion of the central composite design:
\( \alpha = [ \mbox{number of factorial runs} ]^{1/4} \)
If the factorial is a full factorial, then
\( \alpha = \left[ 2^{k} \right] ^{1/4} \)
However, the factorial portion can also be a fractional factorial design
of resolution V.
Table 3.23 illustrates some typical values of
\( \alpha \) as a function of the number of factors.
|
|
Values of
\( \alpha \) depending on the number of factors in the factorial part
of the design
|
TABLE 3.23: Determining
\( \alpha \) for Rotatability
Number of
Factors
|
Factorial
Portion
|
Scaled Value for \( \alpha \)
Relative to ±1
|
|
|
2
|
22
|
22/4 = 1.414
|
|
3
|
23
|
23/4 = 1.682
|
|
4
|
24
|
24/4 = 2.000
|
|
5
|
25-1
|
24/4 = 2.000
|
|
5
|
25
|
25/4 = 2.378
|
|
6
|
26-1
|
25/4 = 2.378
|
|
6
|
26
|
26/4 = 2.828
|
|
|
Orthogonal blocking
|
The value of
\( \alpha \) also depends on whether or not the design is orthogonally
blocked. That is, the question is whether or not the design is divided
into blocks such that the block effects do not affect the estimates of
the coefficients in the second order model.
|
|
Example of both rotatability and orthogonal blocking for two factors
|
Under some circumstances, the value of
\( \alpha \) allows simultaneous rotatability and orthogonality. One
such example for k = 2 is shown below:
|
BLOCK
|
X1
|
X2
|
| |
|
|
|
1
|
-1
|
-1
|
|
1
|
1
|
-1
|
|
1
|
-1
|
1
|
|
1
|
1
|
1
|
|
1
|
0
|
0
|
|
1
|
0
|
0
|
|
2
|
-1.414
|
0
|
|
2
|
1.414
|
0
|
|
2
|
0
|
-1.414
|
|
2
|
0
|
1.414
|
|
2
|
0
|
0
|
|
2
|
0
|
0
|
|
|
Additional central composite designs
|
Examples of other central composite designs
will be given after
Box-Behnken designs are described.
|
