Next Page Previous Page Home Tools & Aids Search Handbook
5. Process Improvement
5.5. Advanced topics
5.5.9. An EDA approach to experimental design

5.5.9.2.

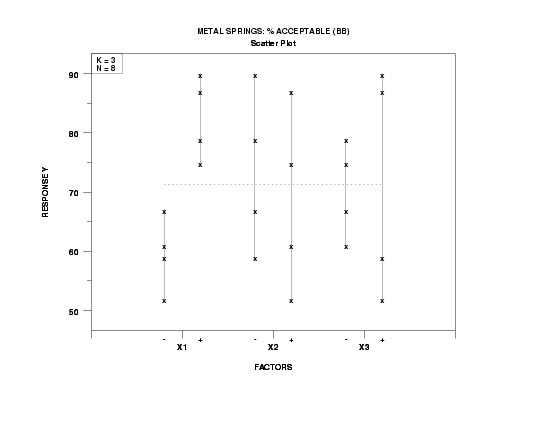
DOE scatter plot
Purpose The DOE (design of experiments) scatter plot answers the following three questions:
  1. What are the most important factors?
  2. What is the best setting for each of these important factors?
  3. What data points are outliers?
In the above questions, the terms "important", "best", and "outliers" need clarification and specificity:

Important

A factor can be "important" if it leads to a significant shift in either the location or the variation of the response variable as we go from the "-" setting to the "+" setting of the factor. Both definitions are relevant and acceptable. The default definition of "important" in engineering/scientific applications is a shift in location. Unless specified otherwise, when a factor is claimed to be important, the implication is that the factor caused a large location shift in the response.

Best

A factor setting is "best" if it results in a typical response that is closest, in location, to the desired project goal (maximization, minimization, target). This desired project goal is an engineering, not a statistical, question, and so the desired optimization goal must be specified by the engineer.

Outlier

A data point is an "outlier" if it comes from a different probability distribution or from a different deterministic model than the remainder of the data. A single outlier in a data set can affect all effect estimates and so in turn can potentially invalidate the factor rankings in terms of importance.

Given the above definitions, the DOE scatter plot is a useful early-step tool for determining the important factors, best settings, and outliers. An alternate name for the DOE scatter plot is "main effects plot".

Output The output for the DOE scatter plot is:
  1. Primary: Identification of the important factors.
  2. Secondary: Best setting for these factors and identification of outliers.
Definition The DOE scatter plot is formed by
  • Vertical Axis: The response (= the raw data) for a given setting (- or +) of a factor for each of the k factors.

  • Horizontal Axis: The k factors, and the two settings (- and +) within each factor.
Motivation The scatter plot is the primary data analysis tool for determining if and how a response relates to another factor. Determining if such a relationship exists is a necessary first step in converting statistical association to possible engineering cause-and-effect. Looking at how the raw data change as a function of the different levels of a factor is a fundamental step which, it may be argued, should never be skipped in any data analysis.

From such a foundational plot, the analyst invariably extracts information dealing with location shifts, variation shifts, and outliers. Such information may easily be washed out by other "more advanced" quantitative or graphical procedures (even computing and plotting means!). Hence there is motivation for the DOE scatter plot.

If we were interested in assessing the importance of a single factor, and since "important" by default means shift in location, then the simple scatter plot is an ideal tool. A large shift (with little data overlap) in the body of the data from the "-" setting to the "+" setting of a given factor would imply that the factor is important. A small shift (with much overlap) would imply the factor is not important.

The DOE scatter plot is actually a sequence of k such scatter plots with one scatter plot for each factor.

Plot for defective springs data The DOE scatter plot for the defective springs data set is as follows.

DOE scatter plot for the defective springs data

How to interpret As discussed previously, the DOE scatter plot is used to look for the following:
  1. Most Important Factors;
  2. Best Settings of the Most Important Factors;
  3. Outliers.
Each of these will be discussed in turn.

Most Important Factors:

For each of the k factors, as we go from the "-" setting to the "+" setting within the factor, is there a location shift in the body of the data? If yes, then

  1. Which factor has the biggest such data location shift (that is, has least data overlap)? This defines the "most important factor".

  2. Which factor has the next biggest shift (that is, has next least data overlap)? This defines the "second most important factor".

  3. Continue for the remaining factors.
In practice, the DOE scatter plot will typically only be able to discriminate the most important factor (largest shift) and perhaps the second most important factor (next largest shift). The degree of overlap in remaining factors is frequently too large to ascertain with certainty the ranking for other factors.

Best Settings for the Most Important Factors:

For each of the most important factors, which setting ("-" or "+") yields the "best" response?

In order to answer this question, the engineer must first define "best". This is done with respect to the overall project goal in conjunction with the specific response variable under study. For some experiments (e.g., maximizing the speed of a chip), "best" means we are trying to maximize the response (speed). For other experiments (e.g., semiconductor chip scrap), "best" means we are trying to minimize the response (scrap). For yet other experiments (e.g., designing a resistor) "best" means we are trying to hit a specific target (the specified resistance). Thus the definition of "best" is an engineering precursor to the determination of best settings.

Suppose the analyst is attempting to maximize the response. In such a case, the analyst would proceed as follows:

  1. For factor 1, for what setting (- or +) is the body of the data higher?
  2. For factor 2, for what setting (- or +) is the body of the data higher?
  3. Continue for the remaining factors.
The resulting k-vector of best settings:
    (x1best, x2best, ..., xkbest)
is thus theoretically obtained by looking at each factor individually in the DOE scatter plot and choosing the setting (- or +) that has the body of data closest to the desired optimal (maximal, minimal, target) response.

As indicated earlier, the DOE scatter plot will typically be able to estimate best settings for only the first few important factors. Again, the degree of data overlap precludes ascertaining best settings for the remaining factors. Other tools, such as the DOE mean plot, will do a better job of determining such settings.

Outliers:

Do any data points stand apart from the bulk of the data? If so, then such values are candidates for further investigation as outliers. For multiple outliers, it is of interest to note if all such anomalous data cluster at the same setting for any of the various factors. If so, then such settings become candidates for avoidance or inclusion, depending on the nature (bad or good), of the outliers.

Conclusions for the defective springs data The application of the DOE scatter plot to the defective springs data set results in the following conclusions:
  1. Most Important Factors:

    1. X1 (most important);
    2. X2 (of lesser importance);
    3. X3 (of least importance).

    that is,

    • factor 1 definitely looks important;
    • factor 2 is a distant second;
    • factor 3 has too much overlap to be important with respect to location, but is flagged for further investigation due to potential differences in variation.

  2. Best Settings:

      (X1, X2, X3) = (+, -, -) = (+1, -1, -1)

  3. Outliers: None detected.
Home Tools & Aids Search Handbook Previous Page Next Page