Next Page Previous Page Home Tools & Aids Search Handbook
5. Process Improvement
5.6. Case Studies
5.6.1. Eddy Current Probe Sensitivity Case Study

5.6.1.8.

Important Factors and Parsimonious Prediction
Identify Important Factors The two problems discussed in the previous section (important factors and a parsimonious model) will be handled in parallel since determination of one yields the other. In regard to the "important factors", our immediate goal is to take the full subset of seven main effects and interactions and extract a subset that we will declare as "important", with the complementary subset being "unimportant". Seven criteria are discussed in detail in section 1.3.5.18.2 in Chapter 1. The relevant criteria will be applied here. These criteria are not all equally important, nor will they yield identical subsets, in which case a consensus subset or a weighted consensus subset must be extracted.
Criteria for Including Terms in the Model The criteria that we can use in determining whether to keep a factor in the model can be summarized as follows.
  1. Effects: Engineering Significance
  2. Effects: 90 % Numerical Significance
  3. Effects: Statistical Significance
  4. Effects: Normal Probability Plot
  5. Averages: Youden Plot
The first four criteria focus on effect estimates with three numerical criteria and one graphical criterion. The fifth criterion focuses on averages. We discuss each of these criteria in detail in the following sections.

The last section summarizes the conclusions based on all of the criteria.

Effects: Engineering Significance The minimum engineering significant difference is defined as
    \( |\hat{\beta_{i}}| > \Delta \)
where \( |\hat{\beta_{i}}| \) is the absolute value of the parameter estimate (i.e., the effect) and \( \Delta \) is the minimum engineering significant difference. That is, declare a factor as "important" if the effect is greater than some a priori declared engineering difference. We use a rough rule-of-thumb of keeping only those factors whose effect is greater than 10 % of the current production average. In this case, let's say that the average detector has a sensitivity of 1.25 ohms. This suggests that we would declare all factors whose effect is greater than 10 % of 1.25 ohms = 0.125 ohms to be significant from an engineering point of view.

Based on this minimum engineering-significant-difference criterion, we conclude to keep two terms: X1 (1.55125) and X2 (-0.43375).

Effects: 90 % Numerical Significance The 90 % numerical significance criterion is defined as
    \( |\hat{\beta_{i}}| > (max |\hat{\beta_{i}}|) / 10 \)
That is, declare a factor as important if it exceeds 10 % of the largest effect. For the current case study, the largest effect is from X1 (1.55125 ohms), and so 10 % of that is 0.155 ohms. This suggests keeping all factors whose effects exceed 0.155 ohms.

Based on the 90 % numerical criterion, we would keep two terms: X1 (1.55125) and X2 (-0.43375). The X2*X3 term, (0.14875), is just under the cutoff.

Effects: Statistical Significance Statistical significance is defined as
    \( |\hat{\beta_{i}}| > 2\mbox{ s.e.}(\hat{\beta_i}) \)
That is, declare a factor as "important" if its effect is more than 2 standard deviations away from 0 (0, by definition, meaning "no effect"). The difficulty with this is that in order to invoke this rule we need the σ (the standard deviation of an observation).

For the eddy current case study, ignoring three-factor and higher interactions leads to an estimate of σ based on omitting only a single term: the X1*X2*X3 interaction.

Thus for our example, if one assumes that the three-factor interaction is nil and hence represents a single drawing from a population centered at zero, an estimate of the standard deviation of an effect is simply the estimate of the interaction effect (0.07125). Two such effect standard deviations is 0.1425. This rule becomes to keep all \( |\hat{\beta_{i}}| \) > 0.1425. This results in keeping three terms: X1 (1.55125), X2 (-0.43375), and X1*X2 (0.14875).

Effects: Probability Plot The normal probability plot can be used to identify important factors. The following graph shows the normal probability plot of the effects.

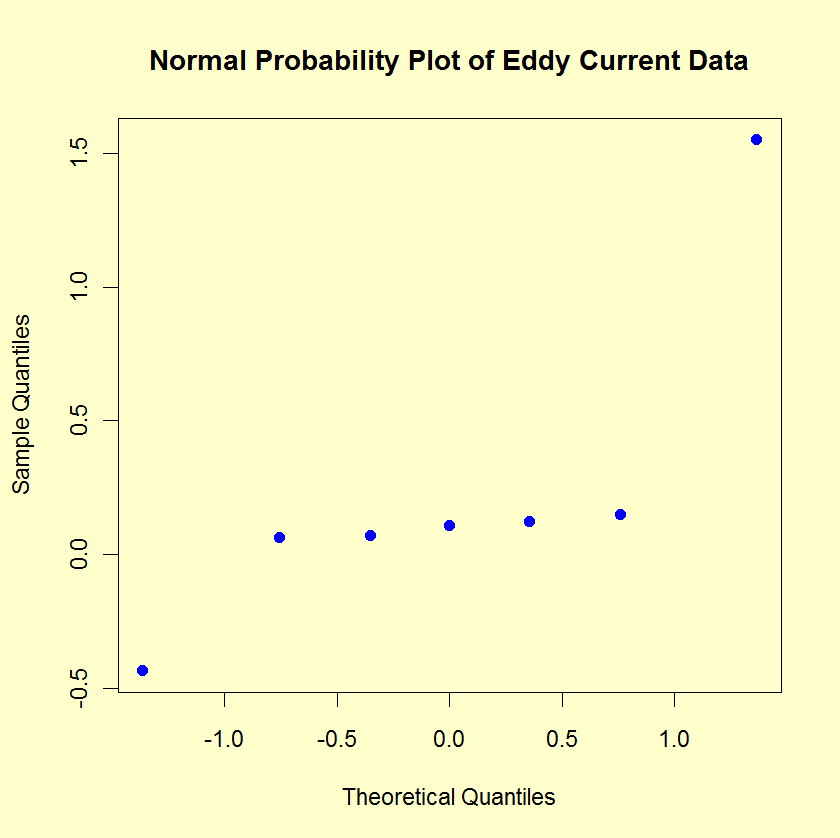
probability plots indicate that model should include main effects for factor 1 and factor 2 with no interaction terms

The normal probablity plot clearly shows two factors displaced off the line, and we see that those two factors are X1 and X2. Thus, we would keep X1 (1.55125) and X2 (-0.43375).

Effects: Youden Plot A DOE Youden plot can be used in the following way. A factor is "important" if it is displaced away from the central-tendency bunch in a Youden plot of high and low averages.

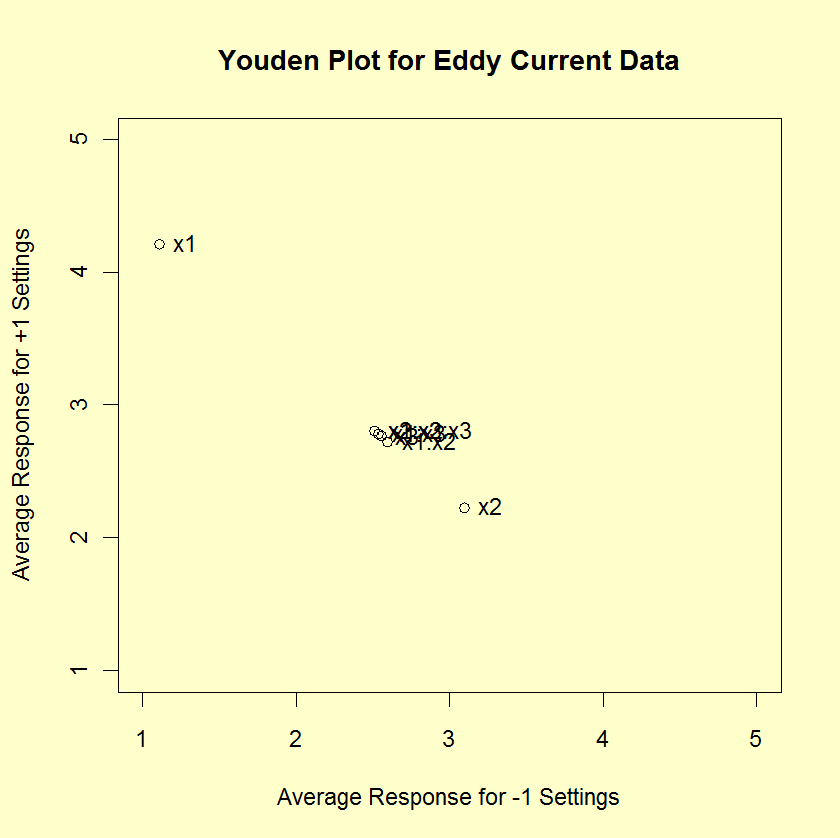
Youden plot show factor 1 and factor 2 main effects stand out

For our example, the Youden plot clearly shows a cluster of points near the grand average (2.65875) with two displaced points above (X1) and below (X2). Based on the Youden plot, we keep two factors: X1 (1.55125) and X2 (-0.43375).

Conclusions In summary, the criterion for specifying "important" factors yielded the following:

  1. Effects, Engineering Significant:
X1 X2
  1. Effects, Numerically Significant:
X1 X2 (X2*X3 is borderline)
  1. Effects, Statistically Significant:
X1 X2 X2*X3
  1. Effects, Normal Probability Plot:
X1 X2
  1. Averages, Youden Plot:
X1 X2

All the criteria select X1 and X2. One also includes the X2*X3 interaction term (and it is borderline for another criteria).

We thus declare the following consensus:

  1. Important Factors: X1 and X2
  2. Parsimonious Prediction Equation:

      \( \hat{Y} = 2.65875 + 1.55125 X_{1} - 0.43375 X_{2} \)

    (with a residual standard deviation of 0.30429 ohms)

Home Tools & Aids Search Handbook Previous Page Next Page