

|
FUNCTION BLOCKName:
LET FUNCTION F = X1**2 LET FUNCTION G = P*(L-X)/(E*I) User defined functions can be used in subsequent commands such as PLOT and LET (basically any place that a built-in Dataplot function can be used). Although Dataplot functions can be powerful, they do have some important limitations for some applications. In particular, Dataplot functions are evaluated on a "row by row" basis. Many statistical applications involve root finding or optimization for functions that involve sums of some kind. Function blocks were introduced to address this limitation. Function blocks allow you to define functions using various Dataplot LET subcommands. Function blocks are created using the CAPTURE syntax. For example,
LET C2 = 1/G LET Y2 = Y**G LET W = Y2*Z LET A1 = SUM W LET A2 = SUM Y2 LET A = C2 - (A1/A2) + C1 END OF CAPTURE The function block contains the following components
The following Dataplot commands can be included in a function block:
The arithmetic operations and statistics LET sub-commands are of particular interest. Commands that are not supported are not added to the function block during the CAPTURE operation. Up to 30 commands can be saved to a given function block. Currently, function blocks can be used with the following commands:
where <one/two/three> specifies which function block is being created; <name> is the name of the function block; <resp> is the name of parameter or a variable that is the result of the function block; and <parameter list> is a list of 1 to 20 parameter names. This syntax is used to create the contents of a function block.
where <one/two/three> specifies which function block is being listed. This syntax is used to list the contents of a function block.
let c1 = n*(log(gamma) - gamma*log(sigma)) let c2 = (gamma - 1)*ylogsum let y2 = (y/sigma)**gamma let c3 = sum y2 let a = c1 + c2 - c3 end of capture
. Purpose: Demonstrate the use of function blocks
.
. Step 1: Read the data
.
skip 25
read weibbury.dat y
skip 0
.
. Step 2: Define the function block
.
let n = size y
let z = log(y)
let zsum = sum z
let c1 = zsum/n
.
capture function block one f a g
let c2 = 1/g
let y2 = y**g
let w = y2*z
let a1 = sum w
let a2 = sum y2
let a = c2 - (a1/a2) + c1
end of capture
.
list function block one
The following output is generated.
CONTENTS OF FUNCTION BLOCK ONE:
let c2 = 1/g
let y2 = y**g
let w = y2*z
let a1 = sum w
let a2 = sum y2
let a = c2 - (a1/a2) + c1
NAME FOR FUNCTION BLOCK ONE: F
PARAMETER LIST FOR FUNCTION BLOCK ONE:
PARAMETER 1: G
RESPONSE PARAMETER/VARIABLE: A
.
. Step 3: Plot the function
.
title offset 2
title case asis
label case ais
y1label Function Response A
x1label G Parameter
title Function Block with Plot Command
plot f for g = 2 0.01 20
delete g
.
. Step 3: Now use it to solve an equation
.
let yroot = roots f wrt g for g = 2 20
The following output is generated.
ROOTS OF AN EQUATION
ROOT VARIABLE = G
SPECIFIED LOWER LIMIT OF INTERVAL = 2.0000000000
SPECIFIED UPPER LIMIT OF INTERVAL = 20.0000000000
NUMBER OF ROOTS FOUND IN INTERVAL = 1
ROOT 1 = 8.117599
let ztemp = yroot(1)
.
line dash
drawsdsd 15 0 85 0
drawdsds ztemp 20 ztemp 90
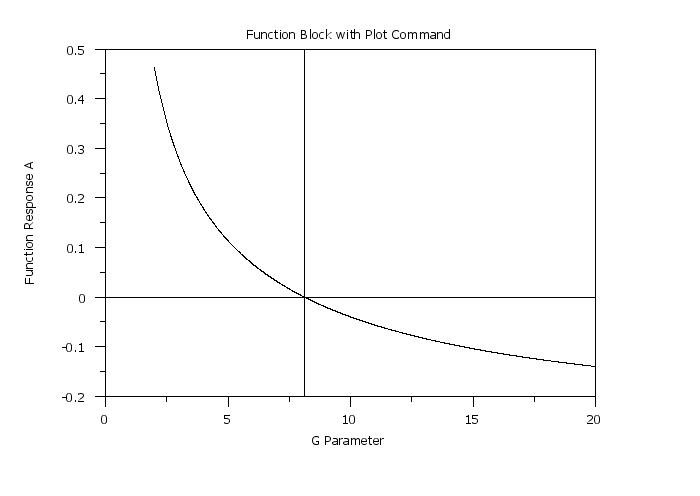
.
let yinte = integral f wrt g for g = 2 6
print yinte
The following output is generated.
PARAMETERS AND CONSTANTS--
YINTE -- 0.8159837E+00
.
let yder = numerical derivative f wrt g for g = 4.2
The following output is generated.
AT X0 = 4.200000 THE DERIVATIVE VALUE = -0.7183620E-01
(WITH ESTIMATED ERROR = 0.8401624E-04)
THE COMPUTED VALUE OF THE CONSTANT YDER = -0.7183620E-01
let gtemp = sequence 2 0.05 6
let yd = numerical derivative f wrt gtemp
y1label Numerical Derivative
plot yd gtemp
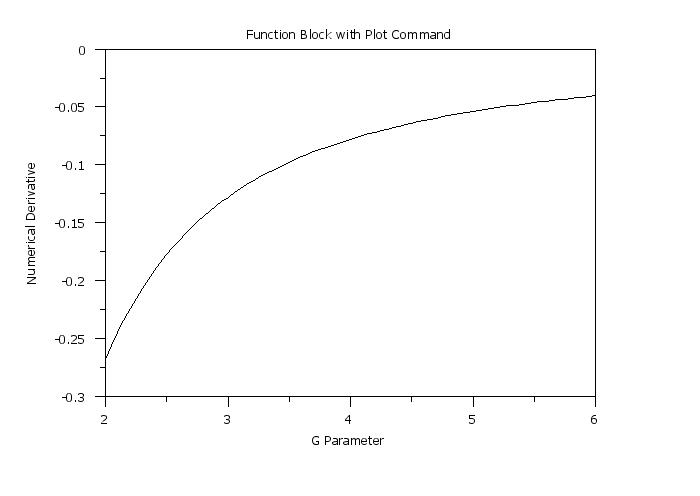 Program 2:
Program 2:
. Purpose: Demonstrate the use of function blocks in univariate
. optimization
.
. Step 1: Read the data
.
skip 25
read weibbury.dat y
skip 0
.
. Step 2: Define the function block
.
set optimization maximum
capture function block one f a gamma
let a = weibull ppcc statistic y
end of capture
.
list function block one
The following output is generated.
CONTENTS OF FUNCTION BLOCK ONE:
let a = weibull ppcc statistic y
NAME FOR FUNCTION BLOCK ONE: F
PARAMETER LIST FOR FUNCTION BLOCK ONE:
PARAMETER 1: GAMMA
RESPONSE PARAMETER/VARIABLE: A
.
. Step 3: Plot the function
.
title offset 2
title case asis
label case ais
y1tic mark offset 0 0.05
tic mark offset units data
y1label PPCC Value
x1label Gamma Parameter
title Function Block for PPCC Statistic
plot f for gamma = 0.10 0.05 50
delete gamma
.
. Step 3: Now use it to perform an optimization
.
let yopt = optimize f wrt gamma for gamma = 0.1 50
The following output is generated.
MINIMUM OF A FUNCTION
OPTIMIZATION VARIABLE = GAMMA
SPECIFIED LOWER LIMIT OF INTERVAL = 0.1000000000
SPECIFIED UPPER LIMIT OF INTERVAL = 50.0000000000
THE MINIMUM VALUE OCCURS AT = 0.3038950E+01
THE COMPUTED VALUE OF THE CONSTANT YOPT = 0.3038950E+01
THE COMPUTED VALUE OF THE CONSTANT FVALUE = -0.9900165E+00
.
line dash
let fvalue = -fvalue
drawsdsd 15 fvalue 85 fvalue
drawdsds yopt 20 yopt 90
.
let gamma = round(yopt,3)
let ppcc = round(fvalue,3)
case asis
just center
move 50 5
text Gamma: ^gamma, PPCC: ^ppcc
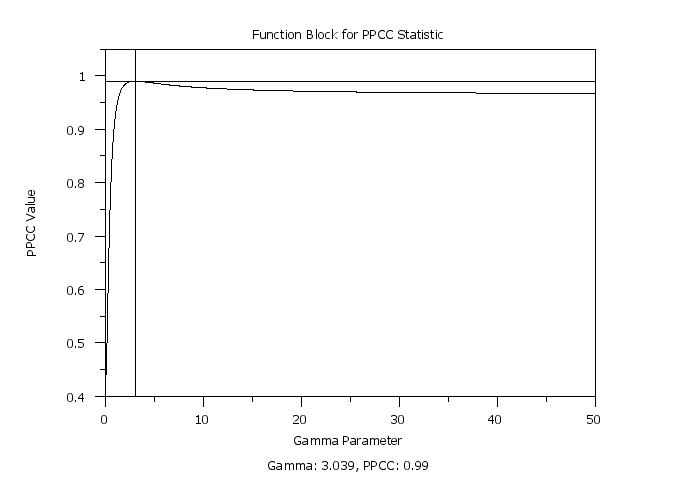 Program 3:
Program 3:
. Purpose: Demonstrate the use of function blocks in multivariate
. optimization
.
. Step 1: Read the data
.
skip 25
read weibbury.dat y
skip 0
.
. Step 2: Define the function block
.
let n = size y
let ylog = log(y)
let ylogsum = sum ylog
let ylsd = sd ylog
let ghat = 1.28/ylsd
let ytemp = y**ghat
let sighat = sum ytemp
let sighat = sighat/n
.
capture function block one f a sigma gamma
let c1 = n*(log(gamma) - gamma*log(sigma))
let c2 = (gamma - 1)*ylogsum
let y2 = (y/sigma)**gamma
let c3 = sum y2
let a = c1 + c2 - c3
end of capture
.
list function block one
The following output is generated.
.
. Step 3: Generate Weibull plot to obtain start values
.
weibull plot y
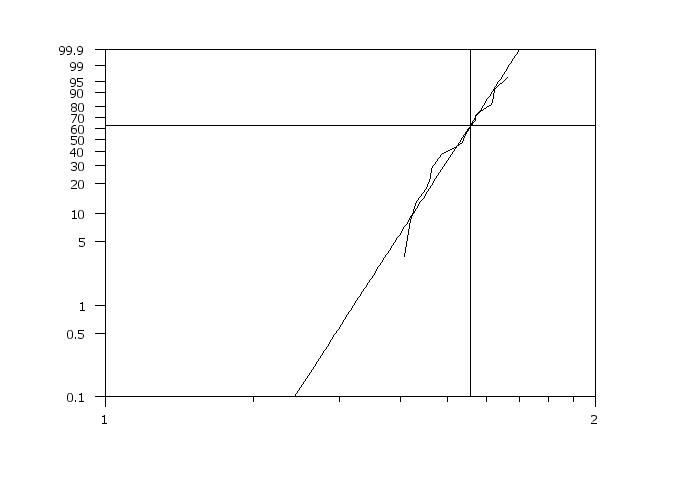
.
. Step 3: Now use it to perform an optimization
.
let gamma = beta
let sigma = eta
set optimization maximum
optimization method line finite
let yopt = optimize f wrt sigma gamma
The following output is generated.
MAXIMUM NUMBER OF ITERATIONS ( 150) EXCEEDED.
THE MINIMUM VALUE OCCURS AT = SIGMA 55.77204
THE MINIMUM VALUE OCCURS AT = GAMMA 8.191590
.
3d-plot f for sigma = 40 0.5 60 for gamma = 5 0.1 10

Date created: 12/01/2015 |
Last updated: 12/11/2023 Please email comments on this WWW page to alan.heckert@nist.gov. | ||||||||||||||||||||||||||