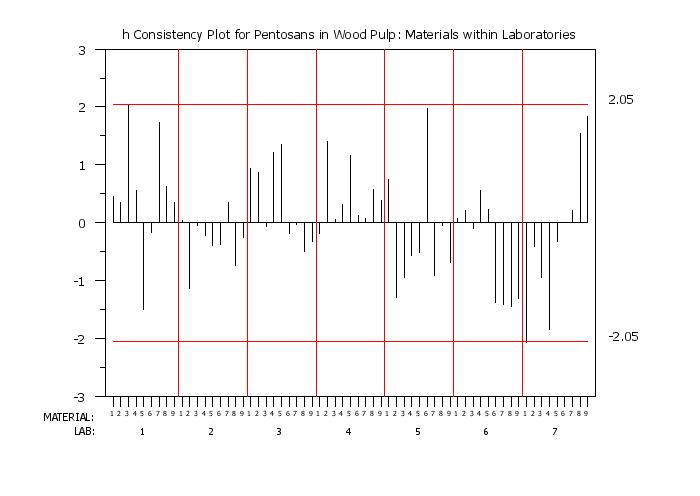
|
H CONSISTENCY PLOT
Name:
| |||||||||||||||||||||||||||||||||||||||||
| CUL | = | the upper critical value (i.e., variance is an outlier if the test statistic is greater than CUL) |
| α | = | the significance level |
| n | = | the number of observations in each group |
| k | = | the number of groups |
| FPPF | = | the percent point function of the F distribution |
Some comments on this test.
't Lam (2009) has extended the Cochran test to support unequal sample sizes and tests for the minimum variance. He refers to this as the G statistic. Dataplot in fact generates the G statistic rather than the C statistic for this test. When the sample sizes are in fact equal, the G statistic for the maximum variance is equivalent to the Cochran C statistic.
The G statistic for the j-th group is
where νi = ni - 1 with ni denoting the sample size of the i-th group.
The critical value for testing the maximum variance is
where
| \( \nu_{pool} \) | = | pooled degrees of freedom |
| = | \( \sum_{i=1}^{k}{\nu_{i}} \) | |
| \( \nu_{j} \) | = | the degrees of freedom corresponding to the maximum variance |
Reject the null hypothesis that the maximum variance is an outlier if the test statistic is greater than the critical value.
The critical value for testing the minimum variance is
In this case, \( \nu_{j} \) corresponds to the minimum variance. Reject the null hypothesis that the minimum variance is an outlier if the test statistic is less than the critical value.
A two-sided test can also be performed. Just use α/2 in place of α in the above formulas. Although the 't Lam article provides a method for determining whether the maximum or minimum variance is more extreme, Dataplot will simply return the test statistic and critical values for both the maximum and the minimum cases.
Note that with the G statistic, we are actually testing for the maximum (or minimum) value of the G statistic rather than the maximum (or minimum) variance. If the sample sizes are equal (or at least approximately equal), this should be equivalent. However, if there is a large difference in sample sizes, this may not be the case. That is, we are testing the maximum \( \nu_{j} s_{j}^{2} \) rather than the maximum \( s_{j}^{2} \).
This syntax plots the h-consistency statistic. The variables must all be of equal length.
This syntax plots the k-consistency statistic. The variables must all be of equal length.
This syntax plots the Cochran variance statistic. The variables must all be of equal length.
LAB: 1 2 3 1 2 3 1 2 3
MAT: 1 1 1 2 2 2 3 3 3
X: 1 2 3 4 5 6 7 8 9
Alternatively, you can stack the lab values so that the x-axis is laid out as
LAB: 1 1 1
2 2 2
3 3 3
MAT: 1 2 3
X: 1 2 3
To specify the stacked alternative, enter the command
To reset the line linear option, enter the command
To defined the x-axis as "materials within laboratories", enter the command
To reset the default, enter
We find it useful to generate both versions of the plot. Although the information being displayed is the same, different types of patterns may be clearer in one or the other of these plots.
where <value> is a non-negative integer. So in the above example,
yields
LAB: 1 2 3 1 2 3 1 2 3
MAT: 1 1 1 2 2 2 3 3 3
X: 1 2 3 5 6 7 9 10 11
Note:
To address this, the following commands were added
These commands allow you to specify the range of laboratories (or materials) to be displayed while still using the full set in computing the statistics. Note that these commands limit you to contiguous ranges of laboratories or materials.
That is, if there are laboratories that are systematically higher or systematically lower than the others, then the test protocol should be carefully examined. Although rejection may be warranted in the case of an obvious error, the real purpose is to improve the underlying measurement process. That is, does the method itself produce consist results with different laboratories? Was the specification of the method clear enough so that different laboratories imnplemented it in a consistent manner?
| H CONSISTENCY STATISTIC | = Compute the h-consistency statistic. |
| K CONSISTENCY STATISTIC | = Compute the k-consistency statistic. |
| COCHRAN VARIANCE OUTLIER TEST | = Perform Cochran's variance outlier test. |
| E691 INTERLAB | = Perform an interlaboratory analysis based on the E691 standard. |
| TWO FACTOR PLOT | = Generate a run sequence plot with two factor variables. |
| TWO WAY ROW PLOT | = Generate a plot based on Mandel's row linear analysis for two-way tables. |
Mandel (1994), "Analyzing Interlaboratory Data According to ASTM Standard E691", Quality and Statistics: Total Quality Management, ASTM STP 1209, Kowalewski, Ed., American Society for Testing and Materials, Philadelphia, PA 1994, pp. 59-70.
Mandel (1993), "Outliers in Interlaboratory Testing", Journal of Testing and Evaluation, Vol. 21, No. 2, pp. 132-135.
Mandel (1995), "Structure and Outliers in Interlaboratory Studies", Journal of Testing and Evaluation, Vol. 23, No. 5, pp. 364-369.
Mandel (1991), "Evaluation and Control of Measurements", Marcel Dekker, Inc..
. Step 1: Read the data
.
skip 25
read mandel6.dat y labid matid
.
. Step 2: Default plot control settings
.
case asis
label case asis
tic mark label case asis
title case asis
title offset 2
.
. Step 3: Plot options
.
let nlab = unique labid
let nmat = unique matid
let ntot = nlab*nmat
.
xlimits 1 ntot
major x1tic mark number ntot
minor x1tic mark number 0
x1tic mark offset 1 1
x1tic mark label off
legend 1 MATERIAL:
legend 2 LAB:
legend 1 justification right
legend 2 justification right
legend 1 coordinates 14 12
legend 2 coordinates 14 15
legend 1 size 1.7
legend 2 size 1.7
spike on
spike base 0
line blank solid solid solid
line color black black red red
.
. Step 4: Generate the plot
.
title h Consistency Plot for Pentosans in Wood Pulp: Laboratories within Materials
h consistency plot y labid matid
.
just left
let atemp = round(hcv,2)
movesd 87 atemp
text ^atemp
let atemp = -atemp
movesd 87 atemp
text ^atemp
.
let ycoorz = 16
let xcoor = 1
justification center
height 1.0
.
loop for k = 1 1 ntot
moveds xcoor ycoorz
let ktemp = mod(k-1,nlab) + 1
text ^ktemp
let xcoor = xcoor + 1
end of loop
.
height 1.5
let ycoorz = 12
let xcoor = (nlab/2)+0.5
line color red
line dash
loop for k = 1 1 nmat
moveds xcoor ycoorz
let ival = k
text ^ival
if k < nmat
let xcoor2 = xcoor + (nlab/2)
drawdsds xcoor2 20 xcoor2 90
end of if
let xcoor = xcoor + nlab
end of loop
line color black
line blank
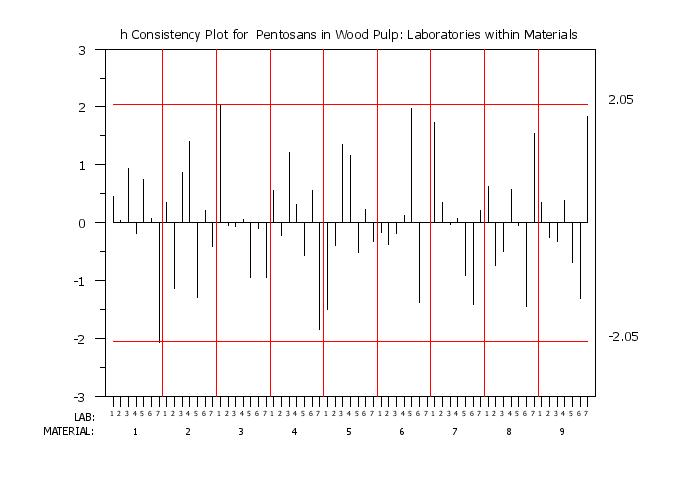 Program 2:
Program 2:
. Step 1: Read the data
.
skip 25
read mandel6.dat y labid matid
.
. Step 2: Default plot control settings
.
case asis
label case asis
tic mark label case asis
title case asis
title offset 2
.
. Step 3: Plot options
.
let nlab = unique labid
let nmat = unique matid
let ntot = nlab*nmat
.
set h consistency plot materials within Laboratories
xlimits 1 ntot
major x1tic mark number ntot
minor x1tic mark number 0
x1tic mark offset 1 1
x1tic mark label off
legend 1 MATERIAL:
legend 2 LAB:
legend 1 justification right
legend 2 justification right
legend 1 coordinates 14 15
legend 2 coordinates 14 12
legend 1 size 1.7
legend 2 size 1.7
spike on
spike base 0
line blank solid solid solid
line color black black red red
.
. Step 4: Generate the plot
.
title h Consistency Plot for Pentosans in Wood Pulp: Materials within Laboratories
h consistency plot y labid matid
.
just left
let atemp = round(hcv,2)
movesd 87 atemp
text ^atemp
let atemp = -atemp
movesd 87 atemp
text ^atemp
.
let ycoorz = 16
let xcoor = 1
justification center
height 1.0
.
loop for k = 1 1 ntot
moveds xcoor ycoorz
let ktemp = mod(k-1,nmat) + 1
text ^ktemp
let xcoor = xcoor + 1
end of loop
.
height 1.5
let ycoorz = 12
let xcoor = (nmat/2)+0.5
line color red
line dash
loop for k = 1 1 nlab
moveds xcoor ycoorz
let ival = k
text ^ival
if k < nlab
let xcoor2 = xcoor + (nmat/2)
drawdsds xcoor2 20 xcoor2 90
end of if
let xcoor = xcoor + nmat
end of loop
line color black
line blank