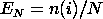SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 1 Vol 2

KOLMOGOROV SMIRNOV GOODNESS OF FIT TEST

Name:
    ... KOLMOGOROV SMIRNOV GOODNESS OF FIT TEST

    NOTE: This command has been replaced with the unified GOODNESS OF FIT command.

Type:
    Analysis Command
Purpose:
    Perform a Kolmogorov-Smirnov goodness of fit test that a set of data come from a hypothesized continuouis distributuion. Dataplot currently supports the Kolmogorov-Smirnov goodness of fit test for 60+ distributions.
Description:
    The Kolmogorov-Smirnov (K-S) test is based on the empirical distribution function (ECDF). Given N data points Y1 Y2 ..., Yn the ECDF is defined as

      E(n) = n(i)/N

    where n(i) is the number of points less than Yi This is a step function that increases by 1/N at the value of each data point.

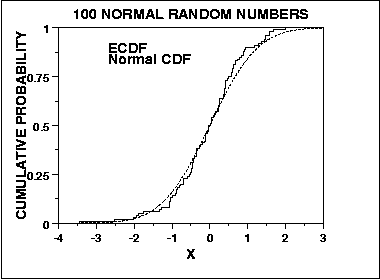
    We can graph a plot of the empirical distribution function with a cumulative distribution function for a given distribution. The K-S test is based on the maximum distance between these two curves. An example of this plot for a sample of 100 normal random numbers is given here.

      plot of ecdf with normal cdf

    An attractive feature of this test is that the distribution of the K-S test statistic itself does not depend on the underlying cumulative distribution function being tested. Another advantage is that it is an exact test (the chi-square goodness of fit depends on an adequate sample size for the approximations to be valid). Despite these advantages, the K-S test has several important limitations:

    1. It only applies to continuous distributions.
    2. It tends to be more sensitive near the center of the distribution than it is at the tails.
    3. Perhaps the most serious limitation is that the distribution must be fully specified. That is, if location, scale, and shape parameters are estimated from the data, the critical region of the K-S test is no longer valid. It typically must be determined by simulation.
    4. The K-S test is only valid for continuous distributions.

    Due to limitations 2 and 3 above, many analysts prefer to use the Anderson-Darling goodness of fit test. However, the Anderson-Darling test is only available for a few specific distributions. In addition, the Anderson-Darling test is more powerful than the K-S test since it makes specific use of the underlying cumulative distribution.

    More formally, the Kolmogorov-Smirnov goodness of fit test statistic can be defined as follows.

    H0: The data follow the specified distribution.
    Ha: The data do not follow the specified distribution.
    Test Statistic: The Kolmogorov-Smirnov goodness of fit test statistic is defined as

      D = max |F(Y(i)) - i/N|

    where F is the theoretical cumulative distribution of the distribution being tested.

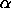
    Significance Level: alpha
    Critical Region: The hypothesis regarding the distributional form is rejected if the test statistic, D, is greater than the critical value obtained from a table. There are several variations of these tables in the literature that use somewhat different scalings for the K-S test statistic and critical regions. These alternative formulations should be equivalent, but it is necessary to ensure that the test statistic is calculated in a way that is consistent with how the critical values were tabulated.

    Dataplot uses the critical values from Chakravart, Laha, and Roy (see Reference: below).

    In order to apply the K-S goodness of fit test, any shape parameters must be specified. For example,

      LET GAMMA = 5.3
      WEIBULL KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST Y

    The name of the distributional parameter for families is given in the list below.

    Location and scale parameters can be specified generically with the following commands:

      LET KSLOC = <value>
      LET KSSCALE = <value>

    The location and scale parameters default to 0 and 1 if not specified.

Syntax:
    <dist> KOLMOGOROV SMIRNOV GOODNESS OF FIT TEST <y> <SUBSET/EXCEPT/FOR/qualification> where <y> is a response variable; <dist> is one of the following distributions:
      1. UNIFORM
      2. SEMI-CIRCULAR
      3. TRIANGULAR
      4. NORMAL
      5. LOGISTIC
      6. DOUBLE EXPONENTIAL
      7. CAUCHY
      8. TUKEY LAMBDA (LAMBDA)
      9. LOGNORMAL (SD, optional, defaults to 1)
      10. HALFNORMAL
      11. T (NU)
      12. CHI-SQUARED (NU)
      13. F (NU1, NU2)
      14. EXPONENTIAL
      15. GAMMA (GAMMA)
      16. BETA (ALPHA, BETA)
      17. WEIBULL (GAMMA)
      18. EXTREME VALUE TYPE 1
      19. EXTREME VALUE TYPE 2 (GAMMA)
      20. PARETO (GAMMA)
      21. WALD (GAMMA)
      22. INVERSE GAUSSIAN (GAMMA)
      23. RIG (GAMMA)
      24. FL (GAMMA)
      25. NONCENTRAL BETA (ALPHA, BETA, LAMBDA)
      26. NONCENTRAL CHISQUARE (NU, LAMBDA)
      27. NONCENTRAL F (NU1, NU2, LAMBDA)
      28. DOUBLY NONCENTRAL F (NU1, NU2, LAMBDA1, LAMBDA2)
      29. NONCENTRAL T (NU, LAMBDA)
      30. DOUBLY NONCENTRAL T (NU, LAMBDA1, LAMBDA2)
      31. HYPERGEOMETRIC (K, N, M)
      32. VON-MISES (B)
      33. POWER-NORMAL (P, SD)
      34. POWER-LOGNORMAL (P, SD)
      35. COSINE
      36. ALPHA (ALPHA, BETA)
      37. POWER FUNCTION (C)
      38. CHI (NU)
      39. LOG LOGISTIC (DELTA)
      40. GENERALIZED GAMMA (GAMMA, C)
      41. ANGLIT
      42. ARCSIN
      43. HYPERBOLIC SECANT
      44. HALF CAUCHY
      45. FOLDED NORMAL (M, SD)
      46. TRUNCATED NORMAL (A, B, M, SD)
      47. TRUNCATED EXPONENTIAL (X0, M, SD)
      48. DOUBLE WEIBULL (GAMMA)
      49. LOG GAMMA (GAMMA)
      50. GENERALIZED EXTREME VALUE (GAMMA)
      51. PARETO SECOND KIND (GAMMA)
      52. HALF LOGISTIC (GAMMA, optional)
      53. EXPONENTIATED WEIBULL (GAMMA, THETA)
      54. GOMPERTZ (C,B)
      55. WRAPPED CAUCHY (C)
      56. BRADFORD (ALPHA, BETA)
      57. DOUBLE GAMMA (GAMMA)
      58. FOLDED CAUCHY (M, SD)
      59. GENERALIZED EXPONENTIAL (LAMBDA1, LAMBDA2, S)
      60. GENERALIZED LOGISTIC (ALPHA)
      61. MIELKE BETA-KAPPA (BETA, THETA, K)
      62. EXPONENTIAL POWER (ALPHA, BETA)
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    NORMAL KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST Y
    NORMAL KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST Y SUBSET GROUP > 1
    CAUCHY KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST Y
    LOGNORMAL KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST X
    EXTREME VALUE TYPE 1 KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST X

    LET LAMBDA = 0.2
    TUKEY LAMBDA KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST X

    SET MINMAX = 1
    LET GAMMA = 2.0
    WEIBULL KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST X

    LET LAMBDA = 3
    POISSON KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST X

    NORMAL KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST Y X
    NORMAL KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST Y X1 X2

Note:
    There are several approaches for estimating the parameters of a distribution before applying the goodness of fit test. PPCC plots combined with probability plots are an effective graphical approach if there are zero or one shape parameters. Maximum likelihood estimation is available for several distributions. Least squares estimation can be applied for distributions for which maximum likelihood estimation is not available.
Note:
    The KOLMOGOROV-SMIRNOV GOODNESS OF FIT command automatically saves the following parameters.

    STATVAL - value of the K-S goodness of fit statistic CUTUPP90 - 90% critical value (alpha = 0.10) for the K-S goodness of fit test statistic CUTUPP95 - 95% critical value (alpha = 0.05) for the K-S goodness of fit test statistic CUTUPP99 - 99% critical value (alpha = 0.01) for the K-S goodness of fit test statistic These parameters can be used in subsequent analysis.

Default:
    Location and scale parameters default to zero and one. Shape parameters must be explicitly specified. There is no default distribution.
Synonyms:
    EV2 and FRECHET are synonyms for EXTREME VALUE TYPE 2.
    EV1 and GUMBEL are synonyms for EXTREME VALUE TYPE 1.
    FATIGUE LIFE is a synonym for FL.
    RECIPROCAL INVERSE GAUSSIAN is a synonym for RIG.
    IG is a synonym for INVERSE GAUSSIAN.
Related Commands:
    ANDERSON-DARLING TEST = Perform Anderson-Darling test for goodness of fit.
    CHI-SQUARE TEST = Perform chi-square test for goodness of fit.
    WILK-SHAPIRO TEST = Perform Wilk-Shapiro test for normality.
    MAXIMUM LIKELIHOOD = Perform maximum likelihood estimation for several distributions.
    FIT = Perform least squares fitting.
    PROBABILITY PLOT = Generates a probability plot.
    HISTOGRAM = Generates a histogram.
    PPCC PLOT = Generates probability plot correlation coefficient plot.
Reference:
    "Handbook of Methods of Applied Statistics, Volume I", Chakravart, Laha, and Roy, John Wiley, 1967, pp. 392-394.
Applications:
    Distributional Analysis
Implementation Date:
    1998/12
Program:
    skip 25
    read zarr13.dat y
    .
    let m = mean y
    let s = standard deviation y
    let ksloc = m
    let ksscale = s
    normal kolmogorov smirnov goodness of fit test y

    The following output is generated. 

     
      ********************************************************
      **  normal kolmogorov-smirnov goodness of fit test y  **
      ********************************************************
 
 
                  KOLMOGOROV-SMIRNOV GOODNESS OF FIT TEST
 
NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
DISTRIBUTION:            NORMAL
   NUMBER OF OBSERVATIONS      =      195
 
TEST:
KOLMOGOROV-SMIRNOV TEST STATISTIC     =   0.3249392E-01
 
   ALPHA LEVEL         CUTOFF              CONCLUSION
           10%        0.08737               ACCEPT H0
            5%        0.09739               ACCEPT H0
            1%        0.11673               ACCEPT H0
Date created: 06/05/2001
Last updated: 12/11/2023
Please email comments on this WWW page to alan.heckert@nist.gov.