

|
MANTEL-HAENSZEL TESTName:
= (N11N22)/ (N12N21) where
N21 = number of failures in sample 1 N12 = number of successes in sample 2 N22 = number of failures in sample 2 The first definition shows the meaning of the odds ratio clearly, although it is more commonly given in the literature with the second definition. The log odds ratio is the logarithm of the odds ratio:
= LOG{(N11N22)/ (N12N21)} Alternatively, the log odds ratio can be given in terms of the proportions
= LOG{(p11p22)/ (p12p21)} where
= proportion of successes in sample 1 p21 = N21/ (N11 + N21) = proportion of failures in sample 1 p12 = N12/ (N12 + N22) = proportion of successes in sample 2 p22 = N22/ (N12 + N22) = proportion of failures in sample 2 Success and failure can denote any binary response. Dataplot expects "success" to be coded as "1" and "failure" to be coded as "0". The bias corrected version of the statistic is:
In addition to reducing bias, this statistic also has the advantage that the odds ratio is still defined even when N12 or N21 is zero (the uncorrected statistic will be undefined for these cases). Note that N11, N21, N12, and N22 defines a 2x2 contingency table. These types of contingency tables are also referred to as fourfold tables. Fleiss, Levin, and Paik also use the following formulation for the ith 2x2 table:
where li = mi + ni2 - ni.. The Mantel-Haenszel test can be used to estimate the common odds ratio and to test whether the overall degree of association is significant. It is a consistent estimator in the following two cases:
Define the following quantities
The Mantel-Haenszel estimate of the common odds ratio is
where g denotes the number of groups. An estimate of the variance of \( \log(\hat{\omega}_{\mbox{MH}}) \) is
A confidence interval for the log(odds ratio) is then
where \( \Phi^{-1} \) is the normal percent point function and SE is the standard error of the estimate (= square root of the variance). The Mantel-Haenszel chi-square statistic for the significance of the overall degree of association is
where
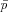 i =
(ni1 Pi1 +
ni2 Pi2)/ni. i =
(ni1 Pi1 +
ni2 Pi2)/ni.
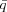 i = 1 - i = 1 -
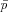 i i
The test statistic is compared to a chi-square distribution with one degree of freedom. The MANTEL-HAENSZEL TEST generates the following output:
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax is used for the case where <y1> and <y2> denote a series of 2x2 tables (i.e., rows 1 and 2 are group 1, rows 3 and 4 are group 2, and so on).
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; <groupid> is a group id variable; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax is used for the case where you have raw data (i.e., the data has not yet been cross tabulated into a two-way table). In this case, the two response variables have an equal number of cases for each group.
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <groupid1> is a group id variable corresponding to <y1>; <y2> is the second response variable; <groupid2> is a group id variable corresponding to <y2>; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax is used for the case where you have raw data (i.e., the data has not yet been cross tabulated into a two-way table). In this case, the two response variables may have an unequal number of cases for each group, so <y1> and <y2> require different group id variables.
MANTEL-HAENSZEL TEST Y1 Y2 X MANTEL-HAENSZEL TEST Y1 X1 Y2 X2
To read this information into Dataplot, enter
READ DPST1F.DAT SIGLEV LOGLOWCL LOGUPPCL ODDLOWCL ODDUPPCL Dataplot saves the following internal parameters:
let n1 = 105
let n2 = 192
let n3 = 145
let n = n1 + n2 + n3
let x = 3 for i = 1 1 n
let istop = n1 + n2
let x = 2 for i = 1 1 istop
let x = 1 for i = 1 1 n1
.
set statistic missing value -99
.
. Group 1 values
.
let y1 = 0 for i = 1 1 n
let y2 = 0 for i = 1 1 n
let y1 = 1 for i = 1 1 81
let y2 = 1 for i = 1 1 34
.
. Group 2 values (have unequal samples here, so fill
. with missing values
.
let istrt = n1 + 1
let istop1 = istrt + 118 - 1
let istop2 = istrt + 69 - 1
let y1 = 1 for i = istrt 1 istop1
let y2 = 1 for i = istrt 1 istop2
let istrt2 = n1 + 174 + 1
let istop2 = n1 + n2
let y2 = -99 for i = istrt2 1 istop2
.
. Group 3 values
.
let istrt = n1 + n2 + 1
let istop1 = istrt + 82 - 1
let istop2 = istrt + 52 - 1
let y1 = 1 for i = istrt 1 istop1
let y2 = 1 for i = istrt 1 istop2
.
mantel haenszel test y1 y2 x
The following output is generated.
SUMMARY OF LOG(ODDS RATIO)
| LOG OF STANDARD
| ODDS RATIO ODDS RATIO ERROR
GROUP | O(i) L(i) SE(L(i))
==================================================
1. | 6.894114 1.930668 0.3099319
2. | 2.414514 0.8814980 0.2138429
3. | 2.313836 0.8389067 0.2400251
MANTEL-HAENSZEL TEST
NUMBER OF GROUPS = 3
M-H ESTIMATE OF COMBINED LOG(ODDS RATIO) = 3.004650
M-H STANDARD ERROR OF COMBINED LOG(ODDS RATIO) = 0.1408284
MANTEL-HAENSZEL TEST STATISTIC (ASSOCIATION) = 62.05933
CHI-SQUARE DEGRESS OF FREEDOM = 1
CHI-SQUARE CDF OF TEST STATISTIC = 1.000000
MANTEL-HAENSZEL (CHI-SQUARE) TEST FOR OVERALL DEGREE OF ASSOCIATION
NULL HYPOTHESIS NULL
NULL CONFIDENCE CRITICAL ACCEPTANCE HYPOTHESIS
HYPOTHESIS LEVEL VALUE INTERVAL CONCLUSION
===================================================================
NO ASSOCIATION 50.0% 0.45 (0,0.500) REJECT
NO ASSOCIATION 80.0% 1.64 (0,0.800) REJECT
NO ASSOCIATION 90.0% 2.71 (0,0.900) REJECT
NO ASSOCIATION 95.0% 3.84 (0,0.950) REJECT
NO ASSOCIATION 97.5% 5.02 (0,0.975) REJECT
NO ASSOCIATION 99.0% 6.63 (0,0.990) REJECT
LARGE SAMPLE CONFIDENCE INTERVAL FOR LOG(ODDS RATIO)
LOG(ODDS RATIO) ODDS RATIO
( 3.004650 ) ( 20.17915 )
CONFIDENCE LOWER UPPER LOWER UPPER
VALUE (%) LIMIT LIMIT LIMIT LIMIT
-----------------------------------------------------------------------
50.000 2.90966 3.09964 18.3506 22.1899
80.000 2.82417 3.18513 16.8470 24.1704
90.000 2.77301 3.23629 16.0067 25.4392
95.000 2.72863 3.28067 15.3119 26.5935
97.500 2.68900 3.32030 14.7169 27.6687
99.000 2.64190 3.36740 14.0399 29.0030
Date created: 10/10/2008 |
Last updated: 12/11/2023 Please email comments on this WWW page to alan.heckert@nist.gov. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||