SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 1 Vol 2

PEAKS OVER THRESHOLD PLOT

Name:
    PEAKS OVER THRESHOLD PLOT
Type:
    Graphics Command
Purpose:
    Generates a peaks over threshold plot.
Description:
    In univariate extreme value analysis, there are two basic approaches for extracting the extreme data.

    1. We find the maximum (or minimum) value in equal length intervals. For example, we could extract the maximum wind speed for each year and then develop a distributional model for these yearly maximums.

      This is commonly referred to as the "epochal" method.

    2. An alternative is to define an overall threshold. We then extract all points above that threshold and develop a distributional model for these points. Note that in this case, the number of points extracted in each interval is not necessarily equal.

    The generalized Pareto distribution provides a useful distributional model for univariate extreme value data since it indicates what type of extreme value model is appropriate (\( \gamma \) denotes the shape parameter):

    1. \( \gamma \) = 0

      This is equivalent to an extreme value type I (Gumbel) distribution.

    2. \( \gamma \) > 0

      This is equivalent to an extreme value type II (Frechet) distribution.

    3. \( \gamma \) < 0

      This is equivalent to a reverse Weibull distribution (in Dataplot, this is a Weibull with SET MINMAX MINIMUM). The shape parameter for the reverse Weibull is -1/\( \gamma \).

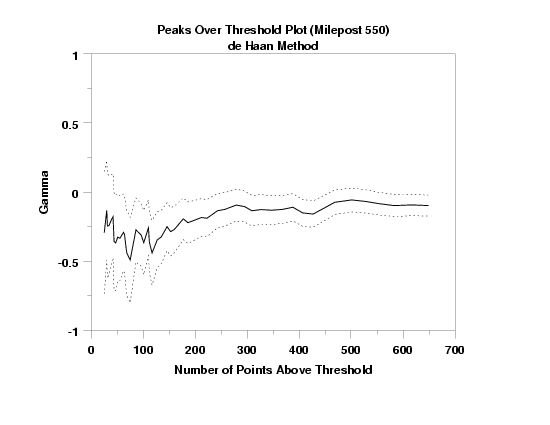
    The purpose of the PEAKS OVER THRESHOLD PLOT is to see how the estimated value of gamma changes as the threshold is changed. Specifically, the plot is generated as follows:

    1. Define an initial threshold. In Dataplot, you can specify either the starting number of points above the threshold or a particular value for the threshold.

      To specify the intial number of points above the threshold, enter the command

        SET PEAKS OVER THRESHOLD INITIAL POINTS

      To specify a starting value for the threshold, enter the command

        SET PEAKS OVER THRESHOLD INITIAL THRESHOLD

      If neither command is given, Dataplot will start with a threshold that gives 2.5% of the data set. If both are specified, the INITIAL THRESHOLD takes precedence over the INITIAL POINTS.

    2. For the points above the threshold, estimate the parameters for the generalized Pareto distribution (see the Note section below for details on how this is done).

      In addition, calculate a confidence interval for the shape parameter. For the de Haan and CME methods (see the Note section below), we compute the standard deviation of the estimate of gamma. We then use

        \( \gamma \pm 2s \gamma \)
      as an estimate of the confidence interval. For the PPCC plot method, the confidence interval is computed using bootstrapping.

    3. Decrement the threshold. To specify how much to decrement the threshold at each interval, enter the command

        SET PEAKS OVER THRESHOLD INCREMENT

      The default increment is -1.

    4. This is repeated for a pre-specified number of iterations. The default number of iterations is 30. To change the number of iterations, enter the command

        SET PEAKS OVER THRESHOLDS ITERATIONS

    The plot then consists of three curves:

    1. The point estimates of gamma.
    2. The lower confidence limit for gamma.
    3. The upper confidence limit for gamma.

    Each of these is plotted against the number of points above the threshold. To have the actual threshold plotted on the horizontal axis, enter the command

      SET PEAKS OVER THRESHOLD X AXIS THRESHOLD

    To restore the default of the number of points above the threshold, enter the command

      SET PEAKS OVER THRESHOLD X AXIS POINTS

    The basic interpretation of this plot is:

      When the threshold is high, few points are included so the variance of gamma is also high (and so the resulting confidence intervals are wide). As the threshold decreases (and more points are included), the variance of gamma decreases with resulting narrower confidence intervals. However, as the number of points increases, the bias of the estimate of gamma increases. This will often be indicated by a downward slope of the graph. Over intervals where the bias error is small, the graph will be nearly horizontal. When choosing a reasonable value of gamma from the graph, it should be noted that larger estimates of gamma imply a longer tail and are therefore conservative from a structural engineering point of view.

    In addition to the plot, this command will also generate the following tables at each iteration.

    1. The first table contains the threshold, the number of points above the threshold, and the parameter estimates.

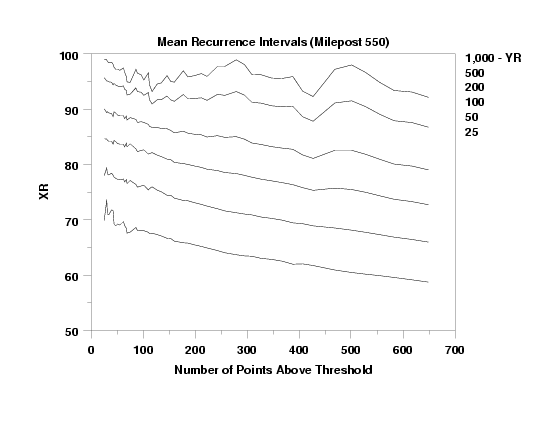
    2. In engineering applications, the mean recurrence interval (this is also referred to as the return interval or recurrence interval) is of interest.

      The return interval of a given wind speed, in years, is defined as the inverse of the probability that the wind speed will be exceeded in any one year. It is defined as

        1/(1 - F(x))

      with F(x) denoting the cumulative distribution function. Mean recurrence intervals are discussed in more detail in Simiu and Scanlon (see References section below).

      More often, we would like to compute the wind speed that corresponds to a given return interval. The solution to this is given by solving the above equation for x.

        X(R) = G(1 - (1/R))

      with G and R denoting the percent point function and the desired mean recurrence interval, respectively.

      The above formula is for the case of a single yearly maximum. If \( \lambda \) is the mean number of threshold crossings per year, the formula is

        \( X(R) = G(1 - (\frac{1}{\lambda R})) \)

      In the Dataplot PEAKS OVER THRESHOLD PLOT command, you can optionally give a second variable that specifies the desired mean recurrence intervals. If you specify mean return intervals, Dataplot will print a table showing the mean return interval along with the corresponding wind speed (called XR).

    3. In wind engineering applications, the load factor is also of interest. This is commonly computed as

        (XMAX/XR50)2

      with XMAX denoting the maximum value of the fitted generalized Pareto distribution (the generalized Pareto is bounded above if the shape parameter is negative) and XR50 denoting the wind speed corresponding to a mean recurrence interval of 50 years.

      To print the value of the maximum wind speed and the load factor, enter the command

        SET PEAKS OVER THRESHOLD LOAD FACTOR OFF

      Since this is specific to extreme wind applications, it is OFF by default.

Syntax 1:
    PEAKS OVER THRESHOLD PLOT <y>
                            <SUBSET/EXCEPT/FOR qualification>
    where <y> is a response variable;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Syntax 2:
    PEAKS OVER THRESHOLD PLOT <y> <r>
                            <SUBSET/EXCEPT/FOR qualification>
    where <y> is a response variable;
                <r> is a variable containing mean recurrence intervals;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    PEAKS OVER THRESHOLD PLOT Y
    PEAKS OVER THRESHOLD PLOT Y R
    PEAKS OVER THRESHOLD PLOT Y SUBSET TAG > 1
Note:
    There are a number of methods for estimating the parameters for the generalized Pareto distribution. To specify the method, enter the command

      SET PEAKS OVER THRESHOLD METHOD <value>

    where <value> is one of the following:

      DEHAAN - use the de Haan method (enter HELP DEHAAN for the details of this method)
      CME - use the conditional mean exceedance method (enter HELP CME for the details of this method)
      PPCC - use the PPCC (probability plot correlation coefficient plot) to estimate gamma and a probability plot to estimate the location and scale parameters. A 95% confidence interval for the gamma parameter is obtained via the bootstrap. For details of these methods, enter HELP PPCC PLOT, HELP PROBABILITY PLOT, and HELP DISTRIBUTIONAL BOOTSTRAP).

      You can obtain more accurate estimates for gamma by restricting the range for the PPCC plot. Enter the commands

        LET GAMMA1 = <lower limit>
        LET GAMMA2 = <upper limit>

      One recommendation is to run the plot with the default limits and then rerun it with tighter limits based on the first plot (be sure to keep them wide enough to accomodate the bootstrap estimates).

    Additional methods will be added in future releases of Dataplot. The default is DEHAAN.

Note:
    Since this command generates a large number of tables, it is typically desired to save them to file. To do this, enter the commands

      CAPTURE POT.OUT
      PEAKS OVER THRESHOLD PLOT Y R
      END OF CAPTURE

    You can alternatively choose to save the output in HTML, Latek, or RTF (Rich Text Format) formats. For example,

      CAPTURE HTML POT.HTM
      PEAKS OVER THRESHOLD PLOT Y R
      END OF CAPTURE

      CAPTURE LATEX POT.TEK
      PEAKS OVER THRESHOLD PLOT Y R
      END OF CAPTURE

      CAPTURE RTF POT.RTF
      PEAKS OVER THRESHOLD PLOT Y R
      END OF CAPTURE

    The HTML and Latex formats can incorporate the plot as well. For details, enter

      HELP CAPTURE HTML
      HELP CAPTURE LATEX
Note:
    Dataplot automatically writes the following values to the file dpst1f.dat (there is one row for each distinct value of the threshold, the following correspond to the columns in dpst1f.dat):

    1. Number of points above the threshold
    2. The threshold
    3. The estimate of the shape parameter, gamma
    4. The estimate of the location parameter
    5. The estimate of the scale parameter

    If mean recurrence intervals have been specified (see Syntax 2), Dataplot additionally writes the following values to the file dpst2f.dat:

    1. Iteration
    2. Number of points above the threshold
    3. The threshold
    4. The requested mean recurrence interval
    5. The XR corresponding to the requested mean recurrence interval
    6. The load factor corresponding to the mean recurrence interval

    Note that the last column, the load factor, is only printed if the SET LOAD FACTOR ON command is entered. This load factor is

      (XR/XR50)2

    A -99.0 is printed for mean recurrence intervals less than or equal to 50.

    The purpose of writing these values to files is to allow you to perform additional analyses. For example, you may want to plot the XR corresponding to the various return intervals. This is demonstrated in the program example below.

Note:
    Some sources reverse the sign in the definition of the generalized Pareto distribution. For details, enter the command

      HELP GEPPDF

    If you use the reversed sign definition, then adjust the role of positive and negative values of gamma in the discussion above.

Default:
    None
Synonyms:
    POT is a synonym for PEAKS OVER THRESHOLD
Related Commands:
    DEHAAN = Compute the estimates for the parameters of the generalized Pareto distribution using the de Haan method.
    CME = Compute the estimates for the parameters of the generalized Pareto distribution using the CME method.
    GEPPPF = Computes the percent point function of the generalized Pareto distribution.
    PPCC PLOT = Generates a ppcc plot.
    PROBABILITY PLOT = Generates a probability plot.
    DISTRIBUTIONAL BOOTSTRAP = Perform a bootstrap analysis for a univariate distribution.
    CME PLOT = Generates a conditional mean exceedance plot.
Reference:
    E. Simiu, N. A. Heckert, and T. Whalen (April, 1996). "Estimates of Hurricane Wind Speeds by the 'Peaks Over Threshold' Method", NIST Technical Note 1416.

    E. Simiu and N. A. Heckert (March 1995). "Extreme Wind Distribution Tails: A 'Peak Over Threshold' Approach", NIST Building Science Series 174.

    Alan Heckert, Emil Simiu, and Tim Whalen (April,1998). "Estimates of Hurricane Wind Speeds by the 'Peaks Over Threshold' Approach", Journal of Structural Engineering, pp. 445-449.

    J. A. Lechner, E. Simiu, N. A. Heckert (1993). "Assessment of 'peak over threshold' Methods for Estimating Extreme Value Distribution Tails", Structural Safety, 12, pp. 305-314.

    E. Simiu and N. A. Heckert (1996). "Extreme Wind Distribution Tails: A 'Peaks Over Threshold' Approach", Journal of Structural Engineering, Vol. 122, No. 5, 1996.

Applications:
    Extreme Value Analysis
Implementation Date:
    2005/5
Program: 
     
DIMENSION 40 COLUMNS
SKIP 2
READ PARAMETER MPOST550.DAT URATE
SKIP 3
READ MPOST550.DAT Y1 TO Y17
.
TITLE Peaks Over Threshold Plot (Milepost 550)CR()de Haan Method
TITLE DISPLACEMENT 5
Y1LABEL Gamma
X1LABEL Number of Points Above Threshold
TITLE CASE ASIS
LABEL CASE ASIS
LINE SOLID DOT DOT
LINE THICKNESS 0.2 0.1 0.1
.
SET PEAKS OVER THRESHOLD ITERATIONS 50
SET PEAKS OVER THRESHOLD PERIOD URATE
SET PEAKS OVER THRESHOLD METHOD DEHAAN
.
LET R = DATA 25 50 100 200 500 1000
.
CAPTURE POT.OUT
PEAKS OVER THRESHOLD PLOT Y17 R
END OF CAPTURE
.
SKIP 0
READ DPST2F.DAT ITER NPOINTS THRESH R2 XR
.
TITLE Mean Recurrence Intervals (Milepost 550)
TITLE DISPLACEMENT 2
Y1LABEL XR
LINE SOLID ALL
LINE THICKNESS 0.1 ALL
.
PLOT XR NPOINTS R2
.
CRLF ON
MARGIN 87
MOVE 87 88
TEXT 1,000 - yr
TEXT 500
TEXT 200
TEXT 100
TEXT 50
TEXT 25
    plot generated by sample program

    plot generated by sample program

Date created: 05/12/2005
Last updated: 12/04/2023
Please email comments on this WWW page to alan.heckert@nist.gov.