

|
PREDICTION LIMITSName:
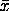 and standard
deviation s, the prediction interval to contain the mean
of m new indpendent, identically distributed observations is and standard
deviation s, the prediction interval to contain the mean
of m new indpendent, identically distributed observations is
with t denoting the percent point function of the t distribution. In this formula, the only value from the new observations is the sample size. That is, it can be applied before the new data is actually collected. The number of observations for the new sample is entered with the command
If NNEW is not defined, then a value of 1 is used. This prediction interval is based on the assumption that the underlying data is approximately normally distributed. However, this prediction interval is fairly robust against non-normality unless either the original sample size or the new sample is small or the departure from normality is severe (in particular, the data is not too skewed). Note that this includes the case of a prediction interval for a single future observation.
<SUBSET/EXCEPT/FOR qualification> where <y> is the response variable; and where the <SUBSET/EXCEPT/FOR qualification> is optional. If LOWER is specified, a one-sided lower prediction limit is returned. If UPPER is specified, a one-sided upper prediction limit is returned. If neither is specified, a two-sided limit is returned. If the keyword LOGNORMAL is present, the log of the data will be taken, then the normal prediction limits will be computed, and then the computed normal lower and upper limits will be exponentiated to obtain the lognormal prediction limits. Similarly, if the keyword BOXCOX is present, a Box-Cox transformation to normality will be applied to the data before computing the normal prediction limits. The computed lower and upper limits will then be transformed back to the original scale. This syntax supports matrix arguments for the response variable.
PREDICTION LIMITS <y1> ... <yk> <SUBSET/EXCEPT/FOR qualification> where <y1> .... <yk> is a list of 1 to 30 response variables; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax will generate a prediction interval for each of the response variables. If LOWER is specified, a one-sided lower prediction limit is returned. If UPPER is specified, a one-sided upper prediction limit is returned. If neither is specified, a two-sided limit is returned. If the keyword LOGNORMAL is present, the log of the data will be taken, then the normal prediction limits will be computed, and then the computed normal lower and upper limits will be exponentiated to obtain the lognormal prediction limits. Similarly, if the keyword BOXCOX is present, a Box-Cox transformation to normality will be applied to the data before computing the normal prediction limits. The computed lower and upper limits will then be transformed back to the original scale. This syntax supports matrix arguments for the response variables.
PREDICTION LIMITS <y> <x1> ... <xk> <SUBSET/EXCEPT/FOR qualification> where <y> is the response variable; <x1> .... <xk> is a list of 1 to 6 group-id variables; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax performs a cross-tabulation of the <x1> ... <xk> and generates a prediction interval for each unique combination of the cross-tabulated values. For example, if X1 has 3 levels and X2 has 2 levels, six prediction intervals will be generated. If LOWER is specified, a one-sided lower prediction limit is returned. If UPPER is specified, a one-sided upper prediction limit is returned. If neither is specified, a two-sided limit is returned. If the keyword LOGNORMAL is present, the log of the data will be taken, then the normal prediction limits will be computed, and then the computed normal lower and upper limits will be exponentiated to obtain the lognormal prediction limits. Similarly, if the keyword BOXCOX is present, a Box-Cox transformation to normality will be applied to the data before computing the normal prediction limits. The computed lower and upper limits will then be transformed back to the original scale. This syntax does not support matrix arguments.
PREDICTION LIMITS Y1 SUBSET TAG > 2 MULTIPLE PREDICTION LIMITS Y1 TO Y5 REPLICATED PREDICTION LIMITS Y X
LET NNEW = 3
LET A = LOWER PREDICTION LIMIT Y
LET A = SUMMARY LOWER PREDICTION LIMIT YMEAN YSD N The first two commands specify the significance level and the number of new observations. The next four commands are used when you have raw data. The last four commands are used when only summary data (mean, standard deviation, sample size) is available. In addition to the above LET command, built-in statistics are supported for 20+ different commands (enter HELP STATISTICS for details).
SKIP 25
READ ZARR13.DAT Y
SET WRITE DECIMALS 5
LET NNEW = 5
.
PREDICTION LIMITS Y
LOWER PREDICTION LIMITS Y
UPPER PREDICTION LIMITS Y
The following output is generated
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Summary Statistics:
Number of Observations: 195
Sample Mean: 9.26146
Sample Standard Deviation: 0.02278
Number of New Observations: 5
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 9.25448 9.26843
80.0 9.24818 9.27473
90.0 9.24440 9.27851
95.0 9.24110 9.28181
99.0 9.23461 9.28831
99.9 9.22697 9.29594
One-Sided Lower Prediction Limits for the Mean
Response Variable: Y
Summary Statistics:
Number of Observations: 195
Sample Mean: 9.26146
Sample Standard Deviation: 0.02278
Number of New Observations: 5
One-Sided Lower Prediction Limits for the Mean
---------------------------
Confidence Lower
Value (%) Limit
---------------------------
50.0 9.26146
80.0 9.25275
90.0 9.24818
95.0 9.24440
99.0 9.23724
99.9 9.22912
One-Sided Upper Prediction Limits for the Mean
Response Variable: Y
Summary Statistics:
Number of Observations: 195
Sample Mean: 9.26146
Sample Standard Deviation: 0.02278
Number of New Observations: 5
One-Sided Upper Prediction Limits for the Mean
---------------------------
Confidence Upper
Value (%) Limit
---------------------------
50.0 9.26146
80.0 9.27016
90.0 9.27473
95.0 9.27851
99.0 9.28567
99.9 9.29379
Program 2:
SKIP 25
READ GEAR.DAT Y X
SET WRITE DECIMALS 5
LET NNEW = 3
REPLICATED PREDICTION LIMITS Y X
The following output is generated
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 1.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99800
Sample Standard Deviation: 0.00434
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99598 1.00001
80.0 0.99404 1.00195
90.0 0.99275 1.00324
95.0 0.99152 1.00447
99.0 0.98870 1.00729
99.9 0.98432 1.01167
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 2.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99910
Sample Standard Deviation: 0.00521
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99668 1.00151
80.0 0.99435 1.00384
90.0 0.99280 1.00539
95.0 0.99133 1.00686
99.0 0.98794 1.01025
99.9 0.98268 1.01551
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 3.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99540
Sample Standard Deviation: 0.00397
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99355 0.99724
80.0 0.99177 0.99902
90.0 0.99060 1.00019
95.0 0.98947 1.00132
99.0 0.98689 1.00390
99.9 0.98288 1.00791
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 4.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99820
Sample Standard Deviation: 0.00385
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99641 0.99998
80.0 0.99469 1.00170
90.0 0.99355 1.00284
95.0 0.99246 1.00393
99.0 0.98995 1.00644
99.9 0.98607 1.01032
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 5.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99190
Sample Standard Deviation: 0.00757
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.98839 0.99540
80.0 0.98500 0.99879
90.0 0.98275 1.00104
95.0 0.98061 1.00318
99.0 0.97568 1.00811
99.9 0.96805 1.01574
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 6.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99879
Sample Standard Deviation: 0.00988
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99422 1.00337
80.0 0.98979 1.00780
90.0 0.98687 1.01072
95.0 0.98407 1.01352
99.0 0.97765 1.01994
99.9 0.96769 1.02990
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 7.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 1.00150
Sample Standard Deviation: 0.00787
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99785 1.00514
80.0 0.99432 1.00867
90.0 0.99199 1.01100
95.0 0.98976 1.01323
99.0 0.98464 1.01835
99.9 0.97671 1.02628
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 8.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 1.00039
Sample Standard Deviation: 0.00362
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99872 1.00207
80.0 0.99709 1.00370
90.0 0.99602 1.00477
95.0 0.99499 1.00580
99.0 0.99264 1.00815
99.9 0.98898 1.01181
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 9.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99829
Sample Standard Deviation: 0.00413
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99638 1.00021
80.0 0.99453 1.00206
90.0 0.99330 1.00329
95.0 0.99213 1.00446
99.0 0.98944 1.00715
99.9 0.98528 1.01131
Two-Sided Prediction Limits for the Mean
Response Variable: Y
Factor Variable 1: X 10.00000
Summary Statistics:
Number of Observations: 10
Sample Mean: 0.99479
Sample Standard Deviation: 0.00532
Number of New Observations: 3
Two-Sided Prediction Limits for the Mean
------------------------------------------
Confidence Lower Upper
Value (%) Limit Limit
------------------------------------------
50.0 0.99233 0.99726
80.0 0.98994 0.99965
90.0 0.98836 1.00123
95.0 0.98686 1.00273
99.0 0.98339 1.00620
99.9 0.97803 1.01156
Program 3:
. Following example from Hahn and Meeker's book.
.
let ymean = 50.10
let ysd = 1.31
let n1 = 5
let nnew = 3
.
set write decimals 5
let slow1 = summary lower prediction limits ymean ysd n1
let supp1 = summary upper prediction limits ymean ysd n1
let slow2 = summary one sided lower prediction limits ymean ysd n1
let supp2 = summary one sided upper prediction limits ymean ysd n1
print slow1 supp1 slow2 supp2
The following output is generated
PARAMETERS AND CONSTANTS--
SLOW1 -- 47.44381
SUPP1 -- 52.75619
SLOW2 -- 48.06049
SUPP2 -- 52.13951
Date created: 04/15/2013 |
Last updated: 12/11/2023 Please email comments on this WWW page to alan.heckert@nist.gov. | ||||||||||||