Dataplot

Vol 2

Vol 1

HOTELLING ONE SAMPLE TSQUARE

Name:

HOTELLING ONE SAMPLE TSQUARE (LET

Type:

Let Subcommand

Purpose:

Compute the 1-sample Hotelling t ² test.

Description:

The 1-sample Hotelling t ² tests the following hypothesis:
H0: U=U0

Here, U0 is a vector of population means, that is, the hypothesized means for each column of the matrix.

The 1-sample t ² test statistic is defined as:

where U₀ is the vector of hypothesized means, 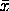contains the sample means for each of the columns, and (1/N) 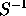is the sample variance-covariance matrix of .

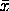T ² is distributed as ((n-1)p/(n-p))F(p,n-p) where n is the number of obserations, p is the number of columns, and F is the F distribution. We reject the null hypothesis if the t ² test statistic is greater than the critical value from the F distribution.

This command returns a parameter that contains the value of the Hotelling t ² test statistic. The critical values corresponding to alpha = .10, .05, .01, and .005 are saved in the internal parameters B90, B95, B99, and B995 respectively.

Syntax:

LET <par> = HOTELLING ONE SAMPLE TSQUARE <mat1> <x>
where <mat1> is a matrix containing the data for the 1-sample Hotelling t ² test;
<x> is a vector containing the hypothesized means;
and where <par> is a parameter where the value of the 1-sample Hotelling t ² test statistic is saved.

Examples:

LET A = 1-SAMPLE HOTELLING T-SQUARE M X

Note:

Matrices are created with either the READ MATRIX command or the MATRIX DEFINITION command. Enter HELP MATRIX DEFINITION and HELP READ MATRIX for details.

Default:

None

Synonyms:

The following are synonyms for HOTELLING ONE SAMPLE TSQUARE:
HOTELLING ONE SAMPLE T2
HOTELLING 1 SAMPLE TSQUARE
HOTELLING 1 SAMPLE T2

Related Commands:

Dataplot Reference Manual
Volume 1: Commands
Auxiliary Chapter

READ MATRIX	= Read a matrix.
MATRIX COLUMN DIMENSION	= Dimension maximum number of columns for Dataplot matrices.
HOTELLING TWO SAMPLE TSQUARE	= Compute the 2-sample Hotelling t 2 test.
QUADRATIC FORM	= Compute the quadratic form of a matrix and a vector.
LINEAR COMBINATION	= Compute a linear combination of a matrix and a vector.

Reference:

"Applied Multivariate Statistical Analysis", Third Edition, Johnson and Wichern, Prentice-Hall, 1992.

Multivariate Analysis

1998/8

DIMENSION 200 COLUMNS
SKIP 25
READ IRIS.DAT SEPLENG SEPWIDTH PETLENG PETWIDTH TAG
SKIP 0
LET NTOT = SIZE SEPLENG
LET M = MATRIX DEFINITION SEPLENG NTOT 4
LET X = DATA 0 0 0 0
LET A = HOTELLING ONE SAMPLE TSQUARE M X
PRINT "1-SAMPLE HOTELLING T-SQUARE TEST STATISTIC = ^A"
PRINT "90% CRITICAL VALUE = ^B90"
PRINT "95% CRITICAL VALUE = ^B95"
PRINT "99% CRITICAL VALUE = ^B99"