Dataplot

Vol 2

Vol 1

HOTELLING TWO SAMPLE TSQUARE

Name:

HOTELLING TWO SAMPLE TSQUARE (LET)

Type:

Let Subcommand

Purpose:

Compute the 2-sample Hotelling t ² test for two matrices.

Description:

The 2-sample Hotelling t² tests the following hypothesis:
H₀: U₁=U₂

Here, U₁ is a vector of population means from sample 1, that is, the hypothesized means for each column of matrix 1. Likewise, U₂ is a vector of population means from sample 2, that is, the hypothesized means for each column of matrix 2.

The 2-sample t ² test statistic is defined as:

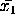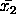where contains the sample means for each of the columns of matrix 1, contains the sample means for each of the columns of matrix 2, N₁ is the sample size for matrix 1, N₂ is the sample size for matrix 2, and 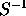is the inverse of the pooled variance-covariance matrices of 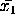and .

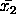T ² is distributed as F(p,n1+n2-p-1) where n1 is the number of obserations for matrix 1, n2 is the number of observations for matrix 2, p is the number of columns (variables), and F is the F distribution. We reject the null hypothesis if the t ² test statistic is greater than the critical value from the F distribution.

This command returns a parameter that contains the value of the Hotelling T ² test statistic. The critical values corresponding to alpha = .10, .05, .01, and .005 are saved in the internal parameters B90, B95, B99, and B995 respectively.

Syntax:

LET <par> = HOTELLING TWO SAMPLE TSQUARE <mat1> <mat2>
where <mat1> is a matrix containing the data for the first sample of the 2-sample Hotelling t ² test;
where <mat2> is a matrix containing the data for the second sample of the 2-sample Hotelling t ² test;
and where <par> is a parameter where the value of the 2-sample Hotelling t ² test statistic is saved.

Examples:

LET A = 2-SAMPLE HOTELLING T-SQUARE M Z

Note:

Matrices are created with either the READ MATRIX command or the MATRIX DEFINITION command. Enter HELP MATRIX DEFINITION and HELP READ MATRIX for details.

Default:

None

Synonyms:

The following are synonyms for HOTELLING TWO SAMPLE TSQUARE:
HOTELLING TWO SAMPLE T2
HOTELLING 2 SAMPLE TSQUARE
HOTELLING 2 SAMPLE T2

Related Commands:

Dataplot Reference Manual
Volume 1: Commands
Auxiliary Chapter

READ MATRIX	= Read a matrix.
MATRIX COLUMN DIMENSION	= Dimension maximum number of columns for Dataplot matrices.
1-SAMPLE HOTELLING T-SQUARE TEST	= Compute the 1-sample Hotelling t-square test.
QUADRATIC FORM	= Compute the quadratic form of a matrix and a vector.
LINEAR COMBINATION	= Compute a linear combination of a matrix and a vector.

Reference:

"Applied Multivariate Statistical Analysis", Third Edition, Johnson and Wichern, Prentice-Hall, 1992.

Multivariate Analysis

1998/8

DIMENSION 200 COLUMNS
SKIP 25
READ IRIS.DAT X1 X2 X3 X4 TAG
SKIP 0
LET Z1 = X1
LET Z2 = X2
LET Z3 = X3
LET Z4 = X4
RETAIN X1 X2 X3 X4 SUBSET TAG = 1
RETAIN Z1 Z2 Z3 Z4 SUBSET TAG = 2
LET N1 = SIZE X1
LET N2 = SIZE Z1
LET M = MATRIX DEFINITION X1 N1 4
LET N = MATRIX DEFINITION Z1 N2 4
LET A = 2-SAMPLE HOTELLING T-SQUARE M N
PRINT "2-SAMPLE HOTELLING T-SQUARE TEST STATISTIC = ^A"
PRINT "90% CRITICAL VALUE = ^B90"
PRINT "95% CRITICAL VALUE = ^B95"
PRINT "99% CRITICAL VALUE = ^B99"