SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

BBNPDF

Name:
    BBNPDF (LET)
Type:
    Library Function
Purpose:
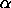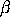    Compute the beta-binomial probability density function with shape parameters alpha, beta, and and N.
Description:
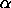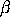    If the probability of success parameter, p, of a binomial distribution has a beta distribution with shape parameters alpha and beta, the resulting distribution is referred to as a beta-binomial distribution. For a standard binomial distribution, p is assumed to be fixed for successive trials. For the beta-binomial distribution, the value of p changes for each trial.

    The beta-binomial distribution has the following probability mass function:

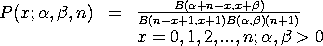
      p(x,alpha,beta,n) = B(alpha+n-x,x+beta)/{(n+1)*B(n-x+1,x+1)* B(alpha,beta)} x = 0, 1, 2, ..., n; alpha, beta > 0

    where B is the complete beta function and alpha and beta are shape parameters.

    Note that some sources reverse the role of alpha and beta in the above formula. In this case, the probability mass function is sometimes given as

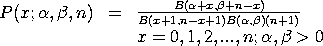
      p(x;alpha,beta,n) = B(alpha+x,beta+n-x)/{B(x+1,n-x+1)* B(alpha,beta)*(n+1)} x = 0, 1, 2, ..., n; alpha, beta > 0
Syntax:
    LET <y> = BBNPDF(<x>,<alpha>,<beta>,<n>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a number, parameter, or variable containing non-negative integer values;
                <alpha> is a number, parameter, or variable that specifies the first shape parameter;
                <beta> is a number, parameter, or variable that specifies the second shape parameter;
                <n> is a number, parameter, or variable that specifies the third shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed beta-binomial pdf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = BBNPDF(10,0.5,0.9,22)
    LET A = BBNPDF(X,2.1,4,N)
    LET X2 = BBNPDF(X1,ALPHA,BETA,N)
Note:
    The beta-binomial as given above is derived as a beta mixture of binomial random variables.

    Alternatively, it can be derived from the Polya urn model for contagion. An urn containing w white balls and b black balls is augmented after each draw of a single ball by c balls of the drawn color (the ball withdrawn is also replaced). X is the total number of white balls drawn after n draws. This is known as the Polya distribution with probability mass function

    P(x;w,b,c,n) = (n x) B(x+w/c,n-x+b/c)/B(w/c,b/c) x = 0, 1, 2, ..., n

    This probability mass function can also be given in the following equivalent forms (given on page 245 of Johnson, Kotz, and Kemp).

    P(x;w,b,c,n) = (n x) (-n-(w+b)/c -x-w/c)/(-(w+b)/c -w/c) x = 0, 1, 2, ..., n

    or

    P(x;w,b,c,n) = (-w/c x) (-b/c n-x)/(-(w+b)/c n) x = 0, 1, 2, ..., n

    The Polya distribution is somewhat more general than the beta-binomial in that the w, b, and c parameters are not restricted to positive numbers. Johnson, Kotz, and Kemp also point out the following special cases of the Polya distribution based on the sign of c.

    1. If c is zero, withdrawals are independent events and the Polya distribution reduces to the binomial distribution.

    2. If c is negative, each withdrawal leads to a reversal of fortune. If w/c is a negative integer, the Polya distribution reduces to the hypergeometric distribution.

    3. If c is positive, both success and failure are contagious. If w/c is a positive integer, the Polya distribution reduces to the negative hypergeometric distribution (if w/c is non-integer, then we have the beta-binomial distribution).

    The forms given here only support the case where w/c and b/c are positive (i.e., the beta-binomial or negative hypergeometric cases).

    Be aware that there are a number of derivations and formulas for the probability mass function for this distribution in the literature. It may be referred to as the inverse hypergeometric distribution, the hypergeometric waiting-time distribution, the Markov-Polya distribution, or the generalized hypergeometric distribution.

Note:
    For a number of commands utilizing the beta-binomial distribution, it is convenient to bin the data. There are two basic ways of binning the data.

    1. For some commands (histograms, maximum likelihood estimation), bins with equal size widths are required. This can be accomplished with the following commands:

        LET AMIN = MINIMUM Y
        LET AMAX = MAXIMUM Y
        LET AMIN2 = AMIN - 0.5
        LET AMAX2 = AMAX + 0.5
        CLASS MINIMUM AMIN2
        CLASS MAXIMUM AMAX2
        CLASS WIDTH 1
        LET Y2 X2 = BINNED

    2. For some commands, unequal width bins may be helpful. In particular, for the chi-square goodness of fit, it is typically recommended that the minimum class frequency be at least 5. In this case, it may be helpful to combine small frequencies in the tails. Unequal class width bins can be created with the commands

        LET MINSIZE = <value>
        LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y

      If you already have equal width bins data, you can use the commands

        LET MINSIZE = <value>
        LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2

      The MINSIZE parameter defines the minimum class frequency. The default value is 5.

Note:
    You can generate beta-binomial random numbers, probability plots, and chi-square goodness of fit tests with the following commands:

      LET N = <value>
      LET ALPHA = <value>
      LET BETA = <value>
      LET Y = BETA BINOMIAL RANDOM NUMBERS FOR I = 1 1 N

      BETA BINOMIAL PROBABILITY PLOT Y
      BETA BINOMIAL PROBABILITY PLOT Y2 X2
      BETA BINOMIAL PROBABILITY PLOT Y3 XLOW XHIGH

      BETA BINOMIAL CHI-SQUARE GOODNESS OF FIT Y
      BETA BINOMIAL CHI-SQUARE GOODNESS OF FIT Y2 X2
      BETA BINOMIAL CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH

    To obtain the maximum likelihood estimates of alpha and beta, enter the command

      BETA BINOMIAL MAXIMUM LIKELIHOOD Y

    Dataplot computes the maximum likelihood estimates using Applied Statistics algorithm 189 written by David Smith (see References below). Note that the Smith algorithm computes the maximum likelihood estimates for the beta-binomial distribution in terms of the parameters mu and theta

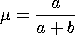
      mu = a/(a+b)

      theta = 1/(a+b)

    Dataplot prints the estimates for both parameterizations.

    You can generate estimates of alpha and beta based on the maximum ppcc value or the minimum chi-square goodness of fit with the commands

      LET N = <value>
      LET ALPHA1 = <value>
      LET ALPHA2 = <value>
      LET BETA1 = <value>
      LET BETA2 = <value>
      BETA BINOMIAL KS PLOT Y
      BETA BINOMIAL KS PLOT Y2 X2
      BETA BINOMIAL KS PLOT Y3 XLOW XHIGH
      BETA BINOMIAL PPCC PLOT Y
      BETA BINOMIAL PPCC PLOT Y2 X2
      BETA BINOMIAL PPCC PLOT Y3 XLOW XHIGH

    The default values of alpha1 and alpha2 are 0.5 and 5, respectively. The default values for beta1 and beta2 are 0.5 and 5, respectively. Due to the discrete nature of the percent point function for discrete distributions, the ppcc plot will not be smooth. For that reason, if there is sufficient sample size the KS PLOT (i.e., the minimum chi-square value) is typically preferred. However, it may sometimes be useful to perform one iteration of the PPCC PLOT to obtain a rough idea of an appropriate neighborhood for the shape parameters since the minimum chi-square statistic can generate extremely large values for non-optimal values of the shape parameters. Also, since the data is integer values, one of the binned forms is preferred for these commands.

Default:
    None
Synonyms:
    None
Related Commands:
    BBNCDF = Compute the beta-binomial cumulative distribution function.
    BBNPPF = Compute the beta-binomial percent point function.
    BETPDF = Compute the beta probability density function.
    BINPDF = Compute the binomial probability mass function.
    BGEPPF = Compute the beta-geometric (Waring) probability mass function.
    BNBPPF = Compute the beta-negative binomial (generalized Waring) probability mass function.
    INTEGER FREQUENCY TABLE = Generate a frequency table at integer values with unequal bins.
    COMBINE FREQUENCY TABLE = Convert an equal width frequency table to an unequal width frequency table.
    KS PLOT = Generate a minimum chi-square plot.
Reference:
    "Empirical Bayes Estimation Of Generator Reliability", Martz, Kvam, and Abramson, Technometrics, February, 1996, pp. 23.

    "Statistical Distributions", 2nd Edition, Evans, Hastings, and Peacock, 1994 (chapter 5).

    "Algorithm AS 189: Maximum Likelihood Estimation of the Parameters of the Beta Binomial Distribution", D. M. Smith, Applied Statistics, 1983, Vol. 32, No. 2.

Applications:
    Distributional Modeling
Implementation Date:
    1996/2
Program: 
     
XLIMITS 0 50
XTIC OFFSET 0.5 0.5
LINE BLANK
SPIKE ON
SPIKE THICKNESS 0.3
.
TITLE CASE ASIS
LABEL CASE ASIS
X1LABEL Number of Successes
Y1LABEL Probability Mass
TITLE DISPLACEMENT 2
Y1LABEL DISPLACEMENT 15
X1LABEL DISPLACEMENT 12
.
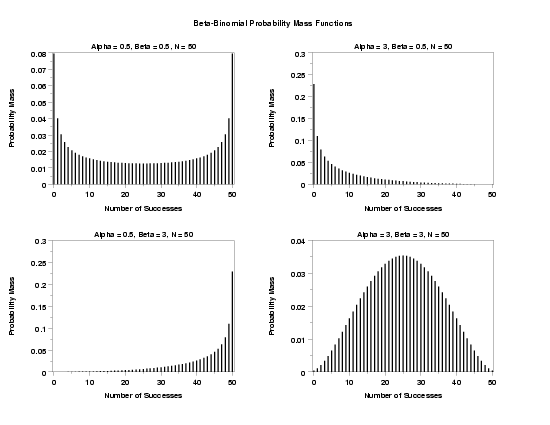
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
TITLE Alpha = 0.5, Beta = 0.5, N = 50
PLOT BBNPDF(X,0.5,0.5,50) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 0.5, N = 50
PLOT BBNPDF(X,3.0,0.5,50) FOR X = 0 1 50
.
TITLE Alpha = 0.5, Beta = 3, N = 50
PLOT BBNPDF(X,0.5,3.0,50) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 3, N = 50
PLOT BBNPDF(X,3.0,3.0,50) FOR X = 0 1 50
.
END OF MULTIPLOT
.
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Beta-Binomial Probability Mass Functions
    plot generated by sample program

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to alan.heckert@nist.gov.