SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

BGECDF

Name:
    BGECDF (LET)
Type:
    Library Function
Purpose:
    Compute the beta-geometric cumulative distribution function with shape parameters alpha and beta.
Description:
    If the probability of success parameter, p, of a geometric distribution has a Beta distribution with shape parameters alpha and beta, the resulting distribution is referred to as a beta-geometric distribution. For a standard geometric distribution, p is assumed to be fixed for successive trials. For the beta-geometric distribution, the value of p changes for each trial.

    The beta-geometric distribution has the following probability density function:

      P(x;alpha,beta) = B(alpha+1,x+beta-1)/B(alpha,beta) x = 1, 2, ...; alpha, beta > 0

    with alpha, beta, and B denoting the two shape parameters and the complete beta function, respectively. See the documentation for the BETA command for a description of the complete beta function.

    Dataplot computes the cumulative distribution function using a recurrence relation given by Hesselager. Hesselager gives the recurrence relation as:

      p(x;alpha,beta) = [(x+alpha-1)/(x+alpha+beta)]*p(x-1;alpha,beta)

    Converting this to the parameterization above yields

      p(x;alpha,beta) = [(x+beta-2)/(x+alpha+beta-1)]*p(x-1;alpha,beta)
Syntax:
    LET <y> = BGECDF(<x>,<alpha>,<beta>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a number, parameter, or variable containing non-negative integer values;
                <alpha> is a number, parameter, or variable that specifies the first shape parameter;
                <beta> is a number, parameter, or variable that specifies the second shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed beta-geometric cdf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = BGECDF(4,0.5,0.9)
    LET A = BGECDF(X,2.1,4)
    PLOT BGECDF(X,ALPHA,BETA) FOR X = 1 1 20
Note:
    Some sources shift this distribution to start at x = 0. In this case, the probability mass function is

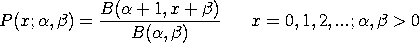
      P(x;alpha,beta) = B(alpha+1,x+beta)/B(alpha,beta) x = 0, 1, 2, ...; alpha, beta > 0

    We will refer to the first parameterization as the unshifted parameterization and the second parameterization as the shifted parameterization.

    To specify the shifted parameterization (i.e., starting at x = 0), enter the command

      SET BETA GEOMETRIC DEFINITION SHIFTED

    To reset the unshifted parameterization (i.e., starting at x = 1), enter the command

      SET BETA GEOMETRIC DEFINITION UNSHIFTED

    This distribution is also sometimes given with alpha and beta reversed. In this case, the probability mass functions become

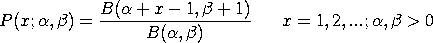
      P(x;alpha,beta) = B(alpha+1,x+beta-1)/B(alpha,beta) x = 1, 2, ...; alpha, beta > 0

      and

      P(x;alpha,beta) = B(alpha+1,x+beta)/B(alpha,beta) x = 0, 1, 2, ...; alpha, beta > 0

    To use this parameterization, simply interchange the order in which you give the alpha and beta arguments to the BGECDF command.
Note:
    The beta-geometric as given above is derived as a beta mixture of geometric random variables.

    Irwin developed the Waring distribution based on the Waring expansion. The probability mass function for the Waring distribution is

      P(x;c,a) = (c-a)*(a+x-1)!*c!/[c*(a-1)!*(c+x)!] x = 0, 1, 2, ...; a > 0; c > a

    The Waring distribution can be computed with the shifted form of the beta-geometric distribution with the following change in parameters:

      beta = a
      alpha = c - a

    If a = 1, then the Waring distribution reduces to the Yule distribution.

    You can compute the Waring (and Yule) distributions using the BGECDF routine with the above re-parameterization or you can use the WARCDF or YULCDF routines directly (enter HELP WARCDF or HELP YULCDF for details).

Default:
    None
Synonyms:
    None
Related Commands:
    BGEPDF = Compute the beta-geometric probability mass function.
    BGECDF Compute the beta-geometric cumulative distribution function.
    BETPDF = Compute the beta probability density function.
    GEOPDF = Compute the geometric probability mass function.
    WARPDF = Compute the Waring probability mass function.
    YULPDF = Compute the Yule probability mass function.
    BBNPDF = Compute the beta-binomial probability mass function.
    BNBPDF = Compute the beta-negative binomial (generalized Waring) probability mass function.
Reference:
    Ole Hesselager (1994), "A Recursive Procedure for Calculations of Some Compound Distributions", Astin Bulliten, Vol. 24, No. 1, pp. 19-32.

    Sudhir R. Paul (2004), "Applications of the Beta Distribution" in "Handbook of the Beta Distribution", edited by Gupta and Nadarajah, Marcel-Dekker, pp. 431-436.

    J. O. Irwin (1963), "The Place of Mathematics in Medical and Biological Statistics", Journal of the Royal Statistical Society, Series A, 126, pp. 1-44.

    Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, chapter 6.

Applications:
    Distributional Modeling
Implementation Date:
    2006/7
Program: 
     
XLIMITS 0 50
XTIC OFFSET 0.5 0.5
LINE BLANK
SPIKE ON
SPIKE THICKNESS 0.3
.
TITLE CASE ASIS
LABEL CASE ASIS
X1LABEL Number of Successes
Y1LABEL Probability
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
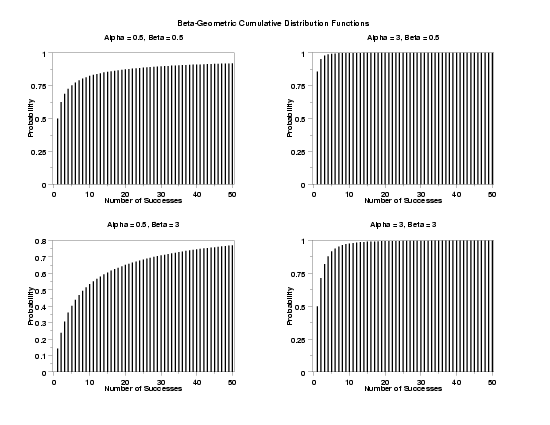
TITLE Alpha = 0.5, Beta = 0.5
PLOT BGECDF(X,0.5,0.5) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 0.5
PLOT BGECDF(X,3.0,0.5) FOR X = 0 1 50
.
TITLE Alpha = 0.5, Beta = 3
PLOT BGECDF(X,0.5,3.0) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 3
PLOT BGECDF(X,3.0,3.0) FOR X = 0 1 50
.
END OF MULTIPLOT
.
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Beta-Geometric Cumulative Distribution Functions
    plot generated by sample program

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to [email protected].