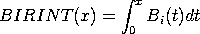BIRINT

BIRINT (LET)

Library Function

This program computes the integral of the Airy function B_i(x).

The BIRINT function is defined as:

with B_i denoting the Airy function of the second kind.

Dataplot computes this function using ACM Algorithm 757 (see Reference: below). The function is computed using Chebyshev expansions, the coefficients of which are given to 20 decimal places.

LET <y> = BIRINT(<x>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, variable or parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed BIRINT function values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = BIRINT(2.3)
PLOT BIRINT(X) FOR X = -5 0.01 5
LET X2 = BIRINT(X1) FOR X1 = 0.1 0.1 3.0

None

None

BAIRY	= Compute the Airy function of the second kind.
AIRY	= Compute the Airy function.
AIRINT	= Compute the integral of the Airy function.
BESSIN	= Compute the modified Bessel function of the first kind and order N.
BESSJN	= Compute the Bessel function of the first kind and order N.
BESSKN	= Compute the modified Bessel function of the third kind and order N.
BESSYN	= Compute the Bessel function of the second kind and order N.
J0INT	= Compute the integral of the Bessel function of the first kind and order 0.
K0INT	= Compute the integral of the modified Bessel function of the third kind and order 0.
Y0INT	= Compute the integral of the Bessel function of the second kind and order 0.

"ACM Transactions of Mathematical Software", Allan MacLead, Vol. 22, No. 3, September, 1996, pp. 288-301.

Special Functions

2005/11

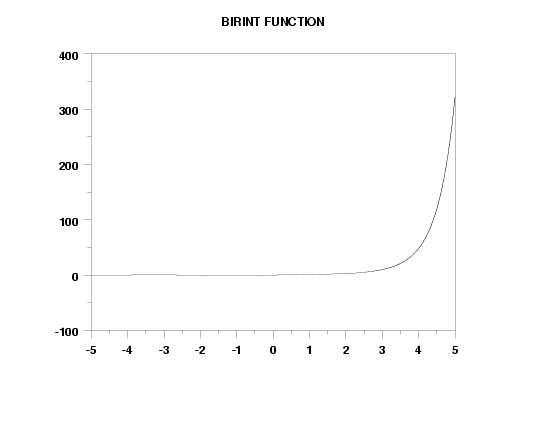
TITLE BIRINT FUNCTION
PLOT BIRINT(X) FOR X = -5 0.01 5