BIWEIGHT SCALE

Name:

BIWEIGHT SCALE (LET) Type:

Let Subcommand Purpose:

Compute a biweight based scale estimate for a variable. Description:

resistance means that changing a small part, even by a large amount, of the data does not cause a large change in the estimate
robustness of efficiency means that the statistic has high efficiency in a variety of situations rather than in any one situation. Efficiency means that the estimate is close to optimal estimate given that we distribution that the data comes from. A useful measure of efficiency is:

Many statistics have one of these properties. However, it can be difficult to find statistics that are both resistant and have robustness of efficiency.

For scale estimaors, the standard deviation (or variance) is the optimal estimator for Gaussian data. However, it is not resistant and it does not have robustness of efficiency. The median absolute deviation (MAD) is a resistant estimate, but it has only modest robustness of efficiency.

The biweight scale estimator is both resistant and robust of efficiency. Mosteller and Tukey recommend using the MAD or interquartile range for exploratory work where moderate efficiency in a variety of situations is adequate. The biweight scale estimator can be considered for situations where high performance is needed.

The biweight scale estimate is defined as:

\( ns_{bi}^2 = \frac{n\sum_{i=1}^{n}{(y - y')^2(1 - u^2)^4}} {(\sum_{i=1}^{n}{(1 - u^2)(1 - 5u^2)})(-1 + \sum_{i=1}^{n}{(1 - u^2)(1 - 5u^2)})} \)

where the summation is restricted to \( u_{i}^2 \le 1 \) and

\( y' = \mbox{median } y \)

and

\( u_{i} = \frac{y_{i} - y'}{9*MAD} \hspace{0.5in} \mbox{for } (\frac{y_{i} - y*}{cS})^{2} < 1 \)

where MAD is the median absolute deviation.

Syntax:

Examples:

Note:

HELP STATISTICS

Default:

None Synonyms:

None Related Commands:

BIWEIGHT MIDVARIANCE	= Compute a biweight midvariance estimate of a variable.
BIWEIGHT LOCATION	= Compute a biweight location estimate of a variable.
BIWEIGHT MIDCOVARIANCE	= Compute a biweight midcovariance estimate of two variables.
BIWEIGHT MIDCORRELATION	= Compute a biweight midcorrelation estimate of two variables.
BIWEIGHT CONFIDENCE LIMITS	= Compute a biweight based confidence interval.
AVERAGE ABSOLUTE DEVIATION	= Compute the average absolute deviation of a variable.
MEDIAN ABSOLUTE DEVIATION	= Compute the median absolute deviation of a variable.
STANDARD DEVIATION	= Compute the standard deviation of a variable.
VARIANCE	= Compute the variance of a variable.
RANGE	= Compute the range of a variable.

Reference:

Data Analysis and Regression: A Second Course in Statistics

Applications:

Robust Data Analysis Implementation Date:

2001/11 Program 1:

 
    LET Y1 = NORMAL RANDOM NUMBERS FOR I = 1 1 10000
    LET Y2 = LOGISTIC RANDOM NUMBERS FOR I = 1 1 10000
    LET Y3 = CAUCHY RANDOM NUMBERS FOR I = 1 1 10000
    LET Y4 = DOUBLE EXPONENTIAL RANDOM NUMBERS FOR I = 1 1 10000
    LET A1 = BIWEIGHT SCALE Y1
    LET A2 = BIWEIGHT SCALE Y2
    LET A3 = BIWEIGHT SCALE Y3
    LET A4 = BIWEIGHT SCALE Y4
    LET B1 = STANDARD DEVIATION Y1
    LET B2 = STANDARD DEVIATION Y2
    LET B3 = STANDARD DEVIATION Y3
    LET B4 = STANDARD DEVIATION Y4
    LET C1 = MAD Y1
    LET C2 = MAD Y2
    LET C3 = MAD Y3
    LET C4 = MAD Y4
    PRINT "BIWEIGHT SCALE     ESTIMATE FOR NORMAL      RANDOM NUMBERS = ^A1"
    PRINT "STANDARD DEVIATION ESTIMATE FOR NORMAL      RANDOM NUMBERS = ^B1"
    PRINT "MAD                ESTIMATE FOR NORMAL      RANDOM NUMBERS = ^C1"
    PRINT " "
    PRINT "BIWEIGHT SCALE     ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = ^A2"
    PRINT "STANDARD DEVIATION ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = ^B2"
    PRINT "MAD                ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = ^C2"
    PRINT " "
    PRINT "BIWEIGHT SCALE     ESTIMATE FOR CAUCHY      RANDOM NUMBERS = ^A3"
    PRINT "STANDARD DEVIATION ESTIMATE FOR CAUCHY      RANDOM NUMBERS = ^B3"
    PRINT "MAD                ESTIMATE FOR CAUCHY      RANDOM NUMBERS = ^C3"
    PRINT " "
    PRINT "BIWEIGHT SCALE     ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = ^A4"
    PRINT "STANDARD DEVIATION ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = ^B4"
    PRINT "MAD                ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = ^C4"

    BIWEIGHT SCALE     ESTIMATE FOR NORMAL      RANDOM NUMBERS = 1.016386
    STANDARD DEVIATION ESTIMATE FOR NORMAL      RANDOM NUMBERS = 0.9975
    MAD                ESTIMATE FOR NORMAL      RANDOM NUMBERS = 0.681249
     
    BIWEIGHT SCALE     ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = 3.066369
    STANDARD DEVIATION ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = 1.817945
    MAD                ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = 1.116496
     
    BIWEIGHT SCALE     ESTIMATE FOR CAUCHY      RANDOM NUMBERS = 3.480419
    STANDARD DEVIATION ESTIMATE FOR CAUCHY      RANDOM NUMBERS = 998.389
    MAD                ESTIMATE FOR CAUCHY      RANDOM NUMBERS = 1.015878
     
    BIWEIGHT SCALE     ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = 1.529625
    STANDARD DEVIATION ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = 1.424258
    MAD                ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = 0.684497

Program 2:

 
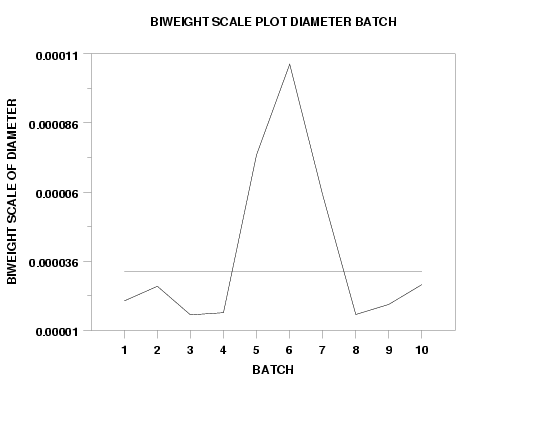
    SKIP 25
    READ GEAR.DAT DIAMETER BATCH
    TITLE AUTOMATIC
    XLIMITS 1 10
    MAJOR XTIC MARK NUMBER 10
    MINOR XTIC MARK NUMBER 0
    XTIC OFFSET 1 1
    X1LABEL BATCH
    Y1LABEL BIWEIGHT SCALE OF DIAMETER
    BIWEIGHT SCALE PLOT DIAMETER BATCH

Program 3:

 
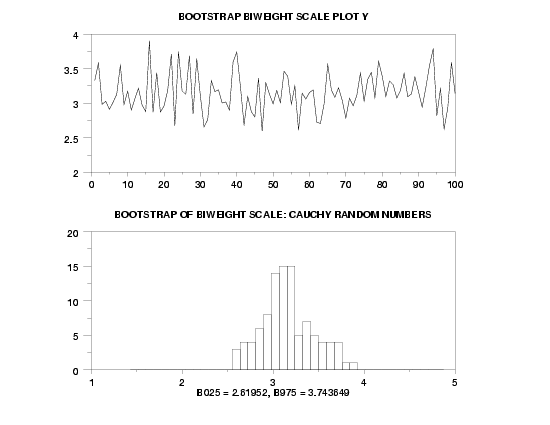
    MULTIPLOT 2 1
    MULTIPLOT CORNER COORDINATES 0 0 100 100
    LET Y = CAUCHY RANDOM NUMBERS FOR I = 1 1 1000
    TITLE AUTOMATIC
    BOOTSTRAP BIWEIGHT SCALE PLOT Y
    X1LABEL B025 = ^B025, B975 = ^B975
    TITLE BOOTSTRAP OF BIWEIGHT SCALE: CAUCHY RANDOM NUMBERS
    HISTOGRAM YPLOT
    END OF MULTIPLOT