BNBPDF

BNBPDF (LET)

Library Function

Compute the beta-negative binomial probability mass function with shape parameters and and k.

If the probability of success parameter, p, of a negative binomial distribution has a Beta distribution with shape parameters and , the resulting distribution is referred to as a beta-negative binomial distribution. For a standard negative binomial distribution, p is assumed to be fixed for successive trials. For the beta-negative binomial distribution, the value of p changes for each trial.

The formula for the beta-negative binomial probability mass function is

with , , and k denoting the shape parameters and denoting the gamma function.

Note that there are a number of different parameterizations and formulations of this distribution in the literature. We use the above formulation because it makes clear the relation between the beta-negative binomial and the negative binomial distributions. It also demonstrates the relation between the beta-negative binomial and the beta-binomial and beta-geometric distributions. It also provides a computationally convenient formula since the beta-negative binomial can be computed as the sums and differences of log gamma functions.

LET <y> = BNBPDF(<x>,<alpha>,<beta>,<k>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, parameter, or variable containing non-negative integer values;
            <alpha> is a number, parameter, or variable that specifies the first shape parameter;
            <beta> is a number, parameter, or variable that specifies the second shape parameter;
            <k> is a number, parameter, or variable that specifies the third shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed beta-negative binomial pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = BNBPDF(4,0.5,0.9,3)
LET A = BNBPDF(X,2.1,4,2.5)
PLOT BNBPDF(X,ALPHA,BETA,K) FOR X = 0 1 20

This distribution is sometimes referred to as the inverse Markov-Polya (or inverse Polya-Eggenberger) distribution.

Irwin developed the generalized Waring distribution based on a generalization of the Waring expansion. The generalized Waring distribution is a re-parameterized beta-negative binomial distribution. Irwin's uses the parameterization

= a
= c - a
k = k

For a number of commands utilizing the beta-negative binomial distribution, it is convenient to bin the data. There are two basic ways of binning the data.
1. For some commands (histograms, maximum likelihood estimation), bins with equal size widths are required. This can be accomplished with the following commands:
   LET AMIN = MINIMUM Y
   LET AMAX = MAXIMUM Y
   LET AMIN2 = AMIN - 0.5
   LET AMAX2 = AMAX + 0.5
   CLASS MINIMUM AMIN2
   CLASS MAXIMUM AMAX2
   CLASS WIDTH 1
   LET Y2 X2 = BINNED
   

2. For some commands, unequal width bins may be helpful. In particular, for the chi-square goodness of fit, it is typically recommended that the minimum class frequency be at least 5. In this case, it may be helpful to combine small frequencies in the tails. Unequal class width bins can be created with the commands
   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
   

   If you already have equal width bins data, you can use the commands

   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2
   

   The MINSIZE parameter defines the minimum class frequency. The default value is 5.

You can generate beta-negative binomial random numbers, probability plots, and chi-square goodness of fit tests with the following commands:
LET K = <value>
LET ALPHA = <value>
LET BETA = <value>
LET Y = BETA NEGATIVE BINOMIAL RANDOM NUMBERS ...
            FOR I = 1 1 N


BETA NEGATIVE BINOMIAL PROBABILITY PLOT Y
BETA NEGATIVE BINOMIAL PROBABILITY PLOT Y2 X2
BETA NEGATIVE BINOMIAL PROBABILITY PLOT Y3 XLOW XHIGH


BETA NEGATIVE BINOMIAL CHI-SQUARE GOODNESS OF FIT Y
BETA NEGATIVE BINOMIAL CHI-SQUARE GOODNESS OF FIT ...
            Y2 X2
BETA NEGATIVE BINOMIAL CHI-SQUARE GOODNESS OF FIT ...
            Y3 XLOW XHIGH

None

GWAPDF is a synonym for BNBPDF

BNBCDF	= Compute the beta-negative binomial cumulative distribution function.
BNBPPF	= Compute the beta-negative binomial percent point function.
BGEPDF	= Compute the beta-geomeric cumulative distribution function.
BETPDF	= Compute the beta probability density function.
NBPDF	= Compute the negative binomial probability mass function.
BBNPDF	= Compute the beta-binomial probability mass function.
INTEGER FREQUENCY TABLE	= Generate a frequency table at integer values with unequal bins.
COMBINE FREQUENCY TABLE	= Convert an equal width frequency table to an unequal width frequency table.
KS PLOT	= Generate a minimum chi-square plot.

Ole Hesselager (1994), "A Recursive Procedure for Calculations of Some Compound Distributions", Astin Bulliten, Vol. 24, No. 1, pp. 19-32.

J. O. Irwin (1975), "The Generalized Waring Distribution Part 1", Journal of the Royal Statistical Society, Series A, 138, pp. 18-31.

J. O. Irwin (1975), "The Generalized Waring Distribution Part 2", Journal of the Royal Statistical Society, Series A, 138, pp. 204-227.

J. O. Irwin (1975), "The Generalized Waring Distribution Part 3", Journal of the Royal Statistical Society, Series A, 138, pp. 374-378.

Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, chapter 6.

Luc Devroye (1992), "Random Variate Generation for the Digamma and Trigamma Distributions", Journal of Statistical Computation and Simulation", Vol. 43, pp. 197-216.

Distributional Modeling

2006/7

 
XLIMITS 0 50
XTIC OFFSET 0.5 0.5
LINE BLANK
SPIKE ON
SPIKE THICKNESS 0.3
.
TITLE CASE ASIS
LABEL CASE ASIS
X1LABEL Number of Successes
Y1LABEL Probability Mass
TITLE DISPLACEMENT 2
Y1LABEL DISPLACEMENT 15
X1LABEL DISPLACEMENT 12
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
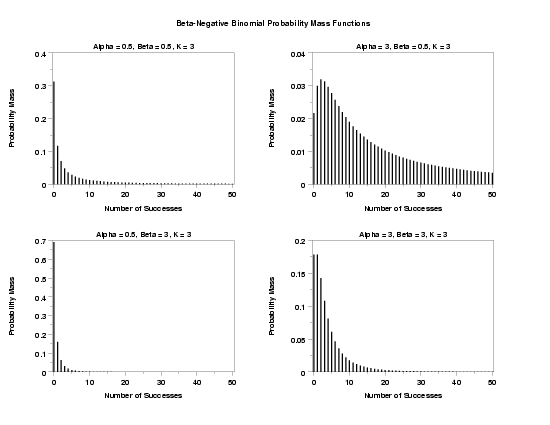
LET K = 3
TITLE Alpha = 0.5, Beta = 0.5, K = 3
PLOT BNBPDF(X,0.5,0.5,K) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 0.5, K = 3
PLOT BNBPDF(X,3.0,0.5,K) FOR X = 0 1 50
.
TITLE Alpha = 0.5, Beta = 3, K = 3
PLOT BNBPDF(X,0.5,3.0,K) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 3, K = 3
PLOT BNBPDF(X,3.0,3.0,K) FOR X = 0 1 50
.
END OF MULTIPLOT
.
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Beta-Negative Binomial Probability Mass Functions
    

 
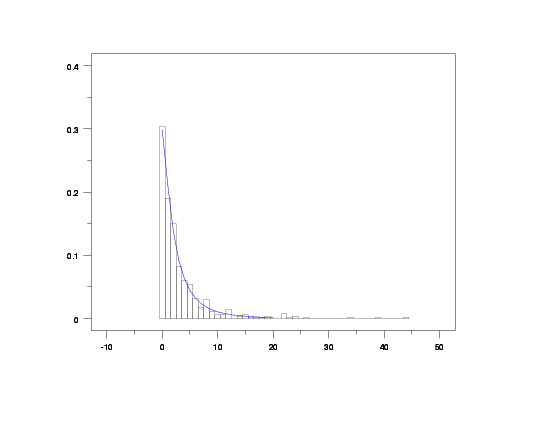
let alpha = 1.5
let beta = 3
let k = 4
.
let y = beta negative binomial random numbers for i = 1 1 500
let amax = maximum y
let amax2 = amax + 0.5
class lower -0.5
class upper amax2
class width 1
let y2 x2 = binned y
let y3 xlow xhigh = integer frequency table y
.
tic offset units screen
tic offset 3 3
.
relative histogram y2 x2
limits freeze
pre-erase off
line color blue
.
plot bnbpdf(x,alpha,beta,k) for x = 0 1 20
limits
pre-erase on
.
beta negative binomial chi-square goodness of fit y3 xlow xhigh
.
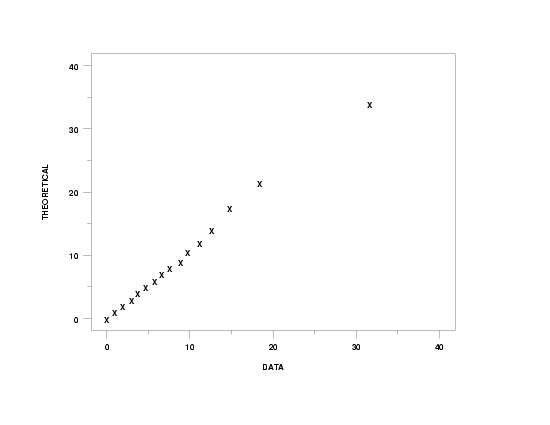
y1label Theoretical
x1label Data
char x
line blank
beta negative binomial probability plot y3 xlow xhigh
    



                   CHI-SQUARED GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            BETA NEGATIVE BINOMIAL
  
 SAMPLE:
    NUMBER OF OBSERVATIONS      =      500
    NUMBER OF NON-EMPTY CELLS   =       16
    NUMBER OF PARAMETERS USED   =        3
  
 TEST:
 CHI-SQUARED TEST STATISTIC     =    17.00824
    DEGREES OF FREEDOM          =       12
    CHI-SQUARED CDF VALUE       =    0.850712
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       18.54935               ACCEPT H0
             5%       21.02607               ACCEPT H0
             1%       26.21697               ACCEPT H0