BTAPDF

BTAPDF (LET)

Library Function

Compute the Borel-Tanner probability density function.

Given a single queue with random arrival times of customers at constant rate l, constant service time , and k initial customers, the Borel-Tanner distribution is the distribution of the total number of customers served before the queue vanishes.

The probability mass function of the Borel-Tanner distribution is

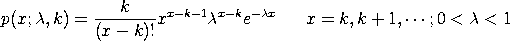
with and k denoting the shape parameters. The k shape parameter is a positive integer and = l .

The mean and variance of the Borel-Tanner distribution are

mean =
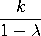
variance =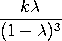

LET <y> = BTAPDF(<x>,<lambda>,<k>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a positive integer variable, number, or parameter;
            <lambda> is a number or parameter in the range (0,1) that specifies the first shape parameter;
            <k> is a number or parameter denoting a positive integer that specifies the first shape parameter;
            <y> is a variable or a parameter where the computed Borel-Tanner pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = BTAPDF(3,0.5,3)
LET Y = BTAPDF(X1,0.3,2)
PLOT BTAPDF(X,0.3,2) FOR X = 2 1 20

For a number of commands utilizing the Borel-Tanner distribution, it is convenient to bin the data. There are two basic ways of binning the data.
1. For some commands (histograms, maximum likelihood estimation), bins with equal size widths are required. This can be accomplished with the following commands:
   LET AMIN = MINIMUM Y
   LET AMAX = MAXIMUM Y
   LET AMIN2 = AMIN - 0.5
   LET AMAX2 = AMAX + 0.5
   CLASS MINIMUM AMIN2
   CLASS MAXIMUM AMAX2
   CLASS WIDTH 1
   LET Y2 X2 = BINNED
   

2. For some commands, unequal width bins may be helpful. In particular, for the chi-square goodness of fit, it is typically recommended that the minimum class frequency be at least 5. In this case, it may be helpful to combine small frequencies in the tails. Unequal class width bins can be created with the commands
   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
   

   If you already have equal width bins data, you can use the commands

   LET MINSIZE = <value>
   LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2
   

   The MINSIZE parameter defines the minimum class frequency. The default value is 5.

You can generate Borel-Tanner random numbers and probability plots with the following commands:
LET N = VALUE
LET K = <value>
LET LAMBDA = <value>
LET Y = BOREL-TANNER RANDOM NUMBERS FOR I = 1 1 N

BOREL TANNER PROBABILITY PLOT Y
BOREL TANNER PROBABILITY PLOT Y2 X2
BOREL TANNER PROBABILITY PLOT Y3 XLOW XHIGH


To obtain the maximum likelihood estimate of lambda assuming that k is known, enter the command

BOREL TANNER MAXIMUM LIKELIHOOD Y
BOREL TANNER MAXIMUM LIKELIHOOD Y2 X2


The maximum likelihood estimate is

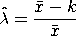
with denoting the sample mean.

For a given value of k, generate an estimate of based on the maximum ppcc value or the minimum chi-square goodness of fit with the commands

LET K = <value>
LET LAMBDA1 = <value>
LET LAMBDA2 = <value>
BOREL TANNER KS PLOT Y
BOREL TANNER KS PLOT Y2 X2
BOREL TANNER KS PLOT Y3 XLOW XHIGH
BOREL TANNER PPCC PLOT Y
BOREL TANNER PPCC PLOT Y2 X2
BOREL TANNER PPCC PLOT Y3 XLOW XHIGH


The default values of LAMBDA1 and LAMBDA2 are 0.05 and 0.95, respectively. The value of k should typically be set to the minimum value of the data. Due to the discrete nature of the percent point function for discrete distributions, the ppcc plot will not be smooth. For that reason, if there is sufficient sample size the KS PLOT (i.e., the minimum chi-square value) is typically preferred. Also, since the data is integer values, one of the binned forms is preferred for these commands.

To generate a chi-square goodness of fit test, enter the commands

LET K = <value>
LET LAMBDA = <value>
BOREL-TANNER CHI-SQUARE GOODNESS OF FIT Y2 X2
BOREL-TANNER CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH

The case where k = 1 is referred to as the Borel distribution. It has probability mass function

If the Borel-Tanner distribution is shifted to start at X = 0 and is reparameterized with
=
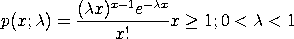
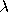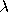
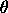= k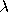

the resulting distribution is referred to as the Lagrange-Poisson distribution (or the Consul generalized Poisson distribution). This distribution has probability mass function

None

None

BTACDF	= Compute the Borel-Tanner cumulative distribution function.
BTAPPF	= Compute the Borel-Tanner percent point function.
POIPDF	= Compute the Poisson probability mass function.
HERPDF	= Compute the Hermite probability mass function.
BINPDF	= Compute the binomial probability mass function.
NBPDF	= Compute the negative binomial mass density function.
GEOPDF	= Compute the geometric probability mass function.
INTEGER FREQUENCY TABLE	= Generate a frequency table at integer values with unequal bins.
COMBINE FREQUENCY TABLE	= Convert an equal width frequency table to an unequal width frequency table.
KS PLOT	= Generate a minimum chi-square plot.
MAXIMUM LIKELIHOOD	= Perform maximum likelihood estimation for a distribution.

Haight and Breuer (1960), "The Borel-Tanner Distribution", Biometrika, 47, pp. 143-150.

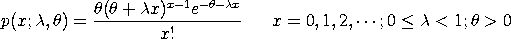
Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, pp. 394-396.

Distributional Modeling

2006/5

 
let k = 2
let lambda = 0.8
let y = borel tanner random numbers for i = 1 1 500
.
let y3 xlow xhigh = integer frequency table y
class lower 1.5
class width 1
let amax = maximum y
let amax2 = amax + 0.5
class upper amax2
let y2 x2 = binned y
.
let k = minimum y
borel tanner mle y
relative histogram y2 x2
limits freeze
pre-erase off
line color blue
plot btapdf(x,lambdaml,k) for x = 2 1 amax
limits
pre-erase on
line color black
let lambda = lambdaml
borel tanner chi-square goodness of fit y3 xlow xhigh
case asis
justification center
move 50 97
text Lambda = ^lambdaml
move 50 93
text Minimum Chi-Square = ^minks, 95% CV = ^cutupp95
.
let k = 2
label case asis
x1label Lambda
y1label Minimum Chi-Square
let lambda1 = 0.5
let lambda2 = 0.9
borel tanner ks plot y3 xlow xhigh
let lambda = shape
borel tanner chi-square goodness of fit y3 xlow xhigh
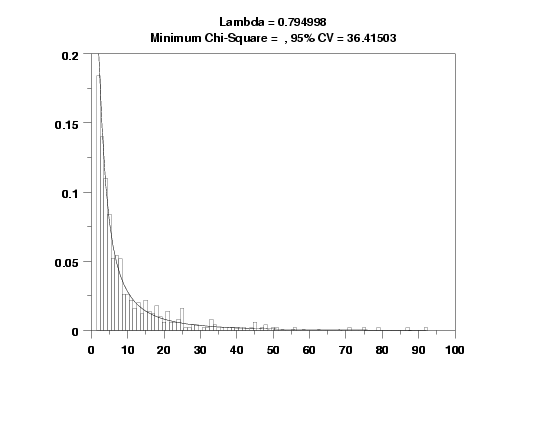
case asis
justification center
move 50 97
text Lambda = ^lambda
move 50 93
text Minimum Chi-Square = ^minks, 95% CV = ^cutupp95
    



                  CHI-SQUARED GOODNESS-OF-FIT TEST
 
NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
DISTRIBUTION:            BOREL-TANNER
 
SAMPLE:
   NUMBER OF OBSERVATIONS      =      500
   NUMBER OF NON-EMPTY CELLS   =       27
   NUMBER OF PARAMETERS USED   =        2
 
TEST:
CHI-SQUARED TEST STATISTIC     =    17.10083
   DEGREES OF FREEDOM          =       24
   CHI-SQUARED CDF VALUE       =    0.155670
 
   ALPHA LEVEL         CUTOFF              CONCLUSION
           10%       33.19624               ACCEPT H0
            5%       36.41503               ACCEPT H0
            1%       42.97982               ACCEPT H0
 
    



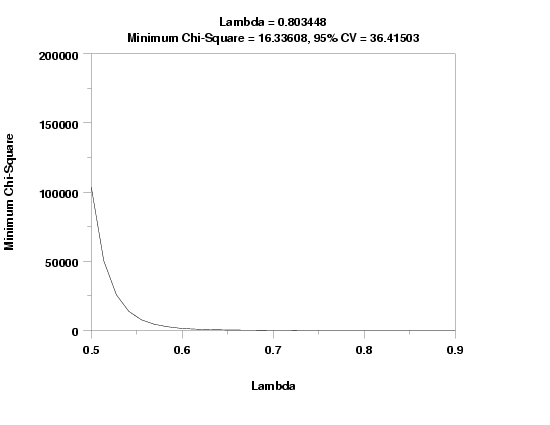
                  CHI-SQUARED GOODNESS-OF-FIT TEST
 
NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
DISTRIBUTION:            BOREL-TANNER
 
SAMPLE:
   NUMBER OF OBSERVATIONS      =      500
   NUMBER OF NON-EMPTY CELLS   =       27
   NUMBER OF PARAMETERS USED   =        2
 
TEST:
CHI-SQUARED TEST STATISTIC     =    16.33608
   DEGREES OF FREEDOM          =       24
   CHI-SQUARED CDF VALUE       =    0.124435
 
   ALPHA LEVEL         CUTOFF              CONCLUSION
           10%       33.19624               ACCEPT H0
            5%       36.41503               ACCEPT H0
            1%       42.97982               ACCEPT H0