CORRELATION

CORRELATION (LET)

Let Subcommand

Compute the correlation coefficient between two variables.

The correlation coefficient is a measure of the linear relationship between two variables. It is computed as:
\( S_{xx} = \sum_{i=1}^{N}{(X_{i}-\bar{X})^2} \)

\( S_{yy} = \sum_{i=1}^{N}{(Y_{i}-\bar{Y})^2} \)

\( S_{xy} = \sum_{i=1}^{N}{(X_{i}-\bar{X}) (Y_{i} - \bar{Y})} \)

\( r = \frac{S_{xy}}{\sqrt{S_{xx}} \sqrt{S_{yy}}} \)

A perfect linear relationship yields a correlation coefficient of +1 (or -1 for a negative relationship) and no linear relationship yields a correlation coefficient of 0.

It may be of interest to determine if the correlation is significantly different than 0. The CDF value for this test is

CDF = FCDF(VAL,1,N-2)

where FCDF is the F cumulative distribution function with 1 and N - 2 degrees of freedom (N is the number of observations) and

\( \mbox{VAL} = \left| \frac{(N-2) r^2}{1 - r^2} \right| \)

with r denoting the computed correlation. The pvalue is 1 - CDF.

LET <par> = CORRELATION <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed correlation is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET <par> = CORRELATION ABSOLUTE VALUE <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the absolute value of the computed correlation is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the absolute value of the correlation coefficient. This is typically used in screening applications where there is an interest in identifying high magnitude correlations regardless of the direction of the correlation.

LET <par> = CORRELATION PVALUE <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed correlation pvalue is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the pvalue (described above) of the correlation.

LET <par> = CORRELATION CDF <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed correlation cdf is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the cdf (described above) of the correlation.

LET A = CORRELATION Y1 Y2
LET A = CORRELATION Y1 Y2 SUBSET TAG > 2

The two variables must have the same number of elements.

Dataplot statistics can be used in a number of commands. For details, enter
HELP STATISTICS

None

None

CORRELATION MATRIX	= Generate a correlation matrix.
RANK CORRELATION	= Compute the rank correlation of two variables.
KENDALLS TAU	= Compute the Kendall tau correlation of two variables.
WINSORIZED CORRELATION	= Compute the Winsorized correlation of two variables.
BIWEIGHT MIDCORRELATION	= Compute the biweight mid-correlation of two variables.
PERCENTAGE BEND CORRELATION	= Compute the percentage bend correlation of two variables.
COVARIANCE	= Compute the covariance of two variables.
PARTIAL CORRELATION	= Compute the partial correlation of three variables.
PARTIAL CORRELATION MATRIX	= Generate the partial correlation matrix.
CORRELATION STAT PLOT	= Generate a correlation vs. subset plot.

Consult any introductory statistics text.

Peavy, Bremer, Varner, Hogben (1986), "OMNITAB 80: An Interpretive System for Statistical and Numerical Data Analysis," NBS Special Publication 701.

Linear Regression

Pre-1987
2011/08: CORRELATION ABSOLUTE VALUE added
2012/06: CORRELATION PVALUE and CORRELATION CDF added

 
SKIP 25
READ BERGER1.DAT Y X
LET CORR = CORRELATION Y X
LET PVAL = CORRELATION PVALUE Y X
LET CDF = CORRELATION CDF Y X
SET WRITE DECIMALS 3
    

The following output is generated.

 PARAMETERS AND CONSTANTS--

    CORR    --          0.946
    PVAL    --          0.000
    CDF     --          1.000
    

 
SKIP 25
READ IRIS.DAT Y1 Y2 Y3 Y4 TAG
.
TITLE CASE ASIS
TITLE OFFSET 2
LABEL CASE ASIS
TIC MARK OFFSET UNITS DATA
Y1LABEL |Correlation|
YLIMITS 0 1
MAJOR YTIC MARK NUMBER 6
MINOR YTIC MARK NUMBER 1
Y1TIC MARK LABEL DECIMAL 1
Y1LABEL DISPLACEMENT 20
X1LABEL Species
XLIMITS 1 3
MAJOR XTIC MARK NUMBER 3
MINOR XTIC MARK NUMBER 0
XTIC MARK OFFSET 0.3 0.3
X1LABEL DISPLACEMENT 14
CHARACTER X BLANK
LINES BLANK SOLID
.
MULTIPLOT CORNER COORDINATES 5 5 95 95
MULTIPLOT SCALE FACTOR 2
MULTIPLOT 2 3
.
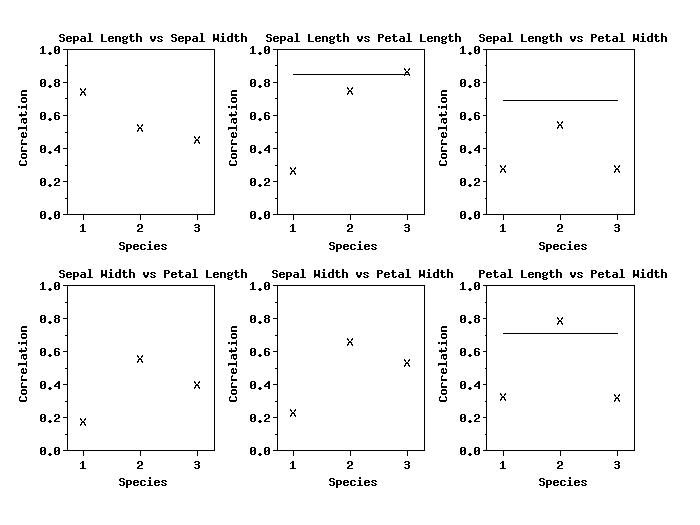
TITLE Sepal Length vs Sepal Width
CORRELATION ABSOLUTE VALUE PLOT Y1 Y2 TAG
.
TITLE Sepal Length vs Petal Length
CORRELATION ABSOLUTE VALUE PLOT Y1 Y3 TAG
.
TITLE Sepal Length vs Petal Width
CORRELATION ABSOLUTE VALUE PLOT Y1 Y4 TAG
.
TITLE Sepal Width vs Petal Length
CORRELATION ABSOLUTE VALUE PLOT Y2 Y3 TAG
.
TITLE Sepal Width vs Petal Width
CORRELATION ABSOLUTE VALUE PLOT Y2 Y4 TAG
.
TITLE Petal Length vs Petal Width
CORRELATION ABSOLUTE VALUE PLOT Y3 Y4 TAG
.
END OF MULTIPLOT