DIFFERENCE OF HODGES-LEHMANN

DIFFERENCE OF HODGES-LEHMANN (LET)

Let Subcommand

Compute the difference between the Hodges-Lehmanns location estimator for two response variables.

The Hodge-Lehmann location estimate is based on ranks. This makes it more resistant, as defined above, than the mean. This estimator also has high efficiency for symmetric disributions. It may be less successful with some skewed distributions.

Specifically, the Hodges-Lehmann estimate for location is defined as

\( \hat{\mu} = \mbox{median} \frac{X_i + X_j} {2} \hspace{0.5in} 1 \le i \le j \le n \)

Dataplot uses ACM algorithm 616 (HLQEST written by John Monohan) to compute the estimate. This is a fast, exact algoirthm. One modification is that for n <= 25 Dataplot computes the estimate directly from the definition.

For the difference of the Hodges-Lehmann location estimats, the Hodges-Lehmann location estimate is computed for each of two samples then their difference is taken.

LET <par> = DIFFERENCE OF HODGES-LEHMANN <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the first response variable;
            <par> is a parameter where the computed difference of the Hodges-Lehmann location estimate is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = DIFFERENCE OF HODGES-LEHMANN Y1 Y2
LET A = DIFFERENCE OF HODGES-LEHMANN Y1 Y2 SUBSET X > 1

Dataplot statistics can be used in a number of commands. For details, enter
HELP STATISTICS

None

None

HODGES-LEHMANN	= Compute the Hodges-Lehmann location estimate.
MEAN	= Compute the mean.
MEDIAN	= Compute the median.
TRIMMED MEAN	= Compute the trimmed mean.
BIWEIGHT LOCATION	= Compute the biweight location.
DIFFERENCE OF MEAN	= Compute the difference of the means.
DIFFERENCE OF MEDIAN	= Compute the difference of the median.
DIFFERENCE OF TRIMMED MEAN	= Compute the difference of the trimmed mean.
DIFFERENCE OF BIWEIGHT LOCATION	= Compute the difference of the biweight location.
STATISTICS PLOT	= Generate a statistic versus subset plot.
BOOTSTRAP PLOT	= Generate a bootstrap plot.
TABULATE	= Perform a tabulation for a specified statistic.

John Monahan (1984), "Algorithm 616: Fast Computation of the Hodges-Lehmann Location Estimator," ACM Transactions on Mathematical Software, Vol. 10, No. 3, pp. 265-270.

Rand Wilcox (1997), "Introduction to Robust Estimation and Hypothesis Testing," Academic Press,

Data Analysis

2003/03

SKIP 25 
READ IRIS.DAT Y1 TO Y4 X 
. 
LET A = DIFFERENCE OF HODGES-LEHMANN Y1 Y2 
TABULATE DIFFERENCE OF HODGES-LEHMANN Y1 Y2 X 
. 
XTIC OFFSET 0.2 0.2 
X1LABEL GROUP ID 
Y1LABEL DIFFERENCE OF HODGES-LEHMANN 
CHAR X 
LINE BLANK 
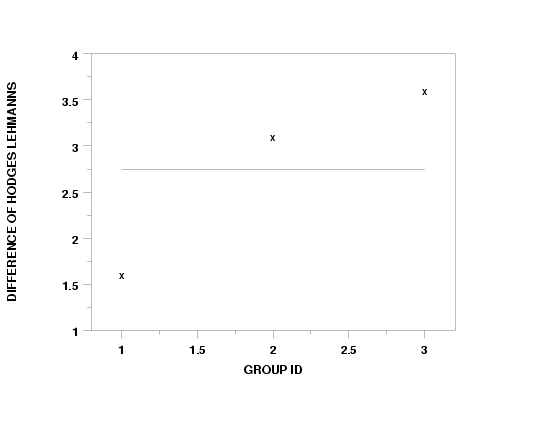
DIFFERENCE OF HODGES-LEHMANN PLOT Y1 Y2 X 
CHAR X ALL 
LINE BLANK ALL 
BOOTSTRAP DIFFERENCE OF HODGES-LEHMANN PLOT Y1 Y2 X  
    

Dataplot generated the following output.

       **************************************************
       **  LET A = DIFFERENCE OF HODGES LEHMANN Y1 Y2  **
       **************************************************
  
  
 THE COMPUTED VALUE OF THE CONSTANT A             =  0.27500002E+01
  
  
       *****************************************************
       **  TABULATE DIFFERENCE OF HODGES LEHMANN Y1 Y2 X  **
       *****************************************************
  
  
                 *    Y1       AND Y2
     X           *    DIFFERENCE OF HODGES-LEHMANN
 **********************************************
     1.00000     *     1.60000
     2.00000     *     3.10000
     3.00000     *     3.60000
  
       GROUP-ID AND STATISTIC WRITTEN TO FILE DPST1F.DAT