

|
DNFPDFName:
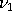 and and
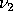 and non-centrality parameters
and non-centrality parameters
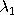 and and
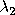 . .
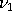 and and
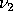 ,
respectively, then ,
respectively, then
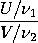
follows a F distribution. If U and V are
replaced with non-central chi-square distributions with
non-centrality parameters
The probability density function of the doubly non-central F distribution is computed by finding the numerical derivative of the doubly non-central F cumulative distribution function. The doubly non-central F distribution can be generalized with location and scale parameters in the usual way.
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, variable or a parameter containing non-negative values; <v1> is a non-negative number, parameter or variable that specifies the first degrees of freedom parameter; <v2> is a non-negative number, parameter or variable that specifies the second degrees of freedom parameter; <lambda1> is a non-negative number, parameter or variable that specifies the first non-centrality parameter; <lambda2> is a non-negative number, parameter or variable that specifies the second non-centrality parameter; <loc> is a number, parameter or variable that specifies the location parameter; <scale> is a number, parameter or variable that specifies the scale parameter; <y> is a variable or a parameter (depending on what <y1> is) where the computed pdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional. Note that the location and scale parameters are optional.
LET A = DNFPDF(2,10,10,5) LET X2 = DNFPDF(1.1,14,15,10000)
The doubly non-central F cumulative distribution function is computed using an algorithm written by Charles Reeves while he was a member of the Statistical Engineering Division at NIST. The algorithm is described in the paper listed in the Reference section below and is based on a series representation given by Bulgren (see the Reference below) of the exact form of the doubly non-central F distribution.
LET NU2 = <value> LET LAMBDA1 = <value> LET LAMBDA2 = <value> LET Y = DOUBLY NON-CENTRAL F RANDOM NUMBERS ...
To generate a non-central F probability plot or an non-central F Kolmogorov-Smirnov or chi-square goodness of fit test, enter the following commands
LET NU2 = <value> LET LAMBDA1 = <value> LET LAMBDA2 = <value> DOUBLY NON-CENTRAL F PROBABILITY PLOT Y DOUBLY NON-CENTRAL F KOLMOGOROV SMIRNOV ...
"On Representations of the Doubly Non-Central F Distribution", W. G. Bulgren, Journal of the the American Statistical Association, Vol. 66, No. 333, 1971 (pp. 184-186). "Continuous Univariate Distributions: Volume 2", Johnson, Kotz, and Balakrishnan, Wiley and Sons, 1994, chapter 30. "Statistical Distributions", Third Edition, Evans, Hastings, and Peacock, 2000 pp. 95-97.
LABEL CASE ASIS
Y1LABEL Probability
X1LABEL X
Y1LABEL DISPLACEMENT 12
X1LABEL DISPLACEMENT 12
TITLE DISPLACEMENT 2
YLIMITS 0 0.9
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
MULTIPLOT 2 2
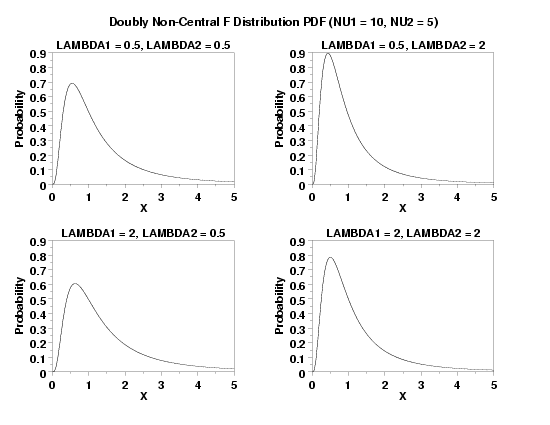
TITLE LAMBDA1 = 0.5, LAMBDA2 = 0.5
PLOT DNFPDF(X,10,5,0.5,0.5) FOR X = 0.01 0.01 5
TITLE LAMBDA1 = 0.5, LAMBDA2 = 2
PLOT DNFPDF(X,10,5,0.5,2) FOR X = 0.01 0.01 5
TITLE LAMBDA1 = 2, LAMBDA2 = 0.5
PLOT DNFPDF(X,10,5,2,0.5) FOR X = 0.01 0.01 5
TITLE LAMBDA1 = 2, LAMBDA2 = 2
PLOT DNFPDF(X,10,5,2,2) FOR X = 0.01 0.01 5
END OF MULTIPLOT
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Doubly Non-Central F Distribution PDF (NU1 = 10, NU2 = 5)
Date created: 7/7/2004 |