

|
DPUPDFName:
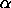 ,
and scale parameter
( ,
and scale parameter
(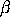 - -
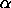 ). ).
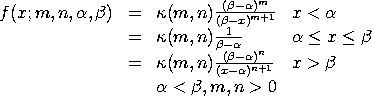
where
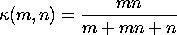
with m and n denoting the shape parameters,
This distribution is uniform between
The case where
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable; <y> is a variable or a parameter (depending on what <x> is) where the computed double Pareto uniform pdf value is stored; <m> is a number, parameter, or variable that specifies the first shape parameter; <n> is a number, parameter, or variable that specifies the second shape paremeter; <alpha> is a number, parameter, or variable that specifies the location parameter; <beta> is a number, parameter, or variable (<beta> - <alpha> is the scale parameter); and where the <SUBSET/EXCEPT/FOR qualification> is optional. If <alpha> and <beta> are omitted, they default to 0 and 1, respectively.
LET Y = DPUPDF(X,1.4,3.2,0,1) PLOT DPUPDF(X,1.4,3.2,-5,5) FOR X = -10 0.1 10
LET N = <value> LET Y = DOUBLY PARETO UNIFORM RANDOM NUMBERS ... FOR I = 1 1 N DOUBLY PARETO UNIFORM PROBABILITY PLOT Y DOUBLY PARETO UNIFORM PROBABILITY PLOT Y2 X2 DOUBLY PARETO UNIFORM PROBABILITY PLOT Y3 XLOW XHIGH DOUBLY PARETO UNIFORM KOLMOGOROV SMIRNOV ... GOODNESS OF FIT Y DOUBLY PARETO UNIFORM CHI-SQUARE ... GOODNESS OF FIT Y2 X2 DOUBLY PARETO UNIFORM CHI-SQUARE ... GOODNESS OF FIT Y3 XLOW XHIGH For the random numbers, you can optionally specify the alpha and beta parameters with the commands
LET BETA = <value> The following commands can be used to estimate the m and n shape parameters for the doubly Pareto uniform distribution:
LET M2 = <value> LET N1 = <value> LET N2 = <value> DOUBLY PARETO UNIFORM PPCC PLOT Y DOUBLY PARETO UNIFORM PPCC PLOT Y2 X2 DOUBLY PARETO UNIFORM PPCC PLOT Y3 XLOW XHIGH DOUBLY PARETO UNIFORM KS PLOT Y DOUBLY PARETO UNIFORM KS PLOT Y2 X2 DOUBLY PARETO UNIFORM KS PLOT Y3 XLOW XHIGH The default values for M1 and M2 are 0.5 and 10. The default values for N1 and N2 are 0.5 and 10.
The probability plot can then be used to estimate the
The following options may be useful for these commands.
The BOOTSTRAP DISTRIBUTION command can be used to find uncertainty intervals for the ppcc plot and ks plot.
Van Dorp, Singh, and Mazzuchi "The Doubly-Pareto Uniform Distribution with Applications in Uncertainty Analysis and Econometrics", Mediterranean Journal of Mathematics, Vol. 3 (2), pp. 205-225.
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
LET ALPHA = 0
LET BETA = 1
.
LET M = 0.5
LET N = 0.5
TITLE M = ^m, N = ^n
PLOT DPUPDF(X,M,N,ALPHA,BETA) FOR X = -5 0.01 5
.
LET M = 2
LET N = 0.5
TITLE M = ^m, N = ^n
PLOT DPUPDF(X,M,N,ALPHA,BETA) FOR X = -5 0.01 5
.
LET M = 0.5
LET N = 2
TITLE M = ^m, N = ^n
PLOT DPUPDF(X,M,N,ALPHA,BETA) FOR X = -5 0.01 5
.
LET M = 2
LET N = 2
TITLE M = ^m, N = ^n
PLOT DPUPDF(X,M,N,ALPHA,BETA) FOR X = -5 0.01 5
.
END OF MULTIPLOT
.
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Doubly Pareto Uniform Probability Density Functions
Program 2:
let alpha = 0
let beta = 1
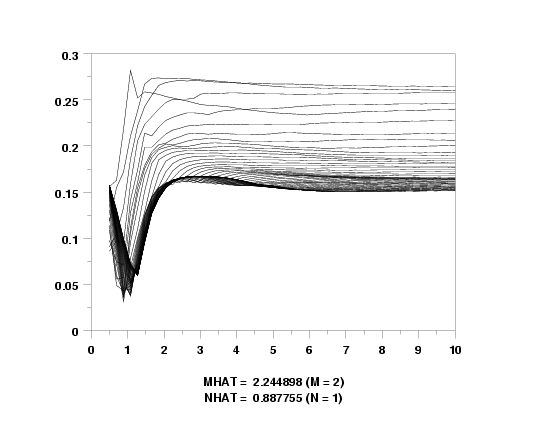
let m = 2
let n = 1
let msav = m
let nsav = n
.
let y = doubly pareto uniform rand numb for i = 1 1 200
.
set ppcc plot location scale biweight
doubly pareto uniform ks plot y
let m = shape1
let n = shape2
justification center
move 50 6
text Mhat = ^m (M = ^msav)
move 50 2
text Nhat = ^n (N = ^nsav)
.
char x
line bl
doubly pareto uniform prob plot y
let alphahat = ppa0bw
let betahat = ppa0bw + ppa1bw
move 50 6
text Alphahat = ^alphahat
move 50 2
text Betahat = ^betahat
char blank
line solid
.
relative hist y
limits freeze
pre-erase off
line color blue
plot dpupdf(x,m,n,alphahat,betahat) for x = -5 0.01 5
line color black
limits
pre-erase on
.
let ksloc = alphahat
let ksscale = betahat - alphahat
doubly pareto uniform kolm smir goodness of fit y
Date created: 1/8/2008 |