GL4PDF

GL4PDF (LET)

Library Function

Compute the type 4 generalized logistic probability density function with shape parameters p and q.

The standard form of the type 4 generalized logistic distribution has the probability density function:

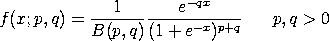
The general form of the type 4 generalized logistic probability density function can be obtained by replacing x in the above formula with (x-loc)/scale.

LET <y> = GL4PDF(<x>,<p>,<q>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, number or parameter;
            <p> is a number or parameter that specifies the value of the first shape parameter;
            <q> is a number or parameter that specifies the value of the second shape parameter;
            <loc> is a number or parameter that specifies the value of the location parameter;
            <scale> is a number or parameter that specifies the value of the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed generalized logistic type 3 pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The location and scale parameters are optional.

LET A = GL4PDF(3,2,0.5)
LET X2 = GL4PDF(X1,P,Q)
PLOT GL4PDF(X,P,Q) FOR X = -5 0.01 5

The generalized logistic type 1, type 2, and type 3 distributions are all special cases of the generalized logistic type 4 distribution.

Generalized logistic type 4 random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET P = <value>
LET Q = <value>
LET Y = GENERALIZED LOGISTIC TYPE 4 RANDOM NUMBERS ...
            FOR I = 1 1 N
GENERALIZED LOGISTIC TYPE 3 PROBABILITY PLOT Y
GENERALIZED LOGISTIC TYPE 3 KOLMOGOROV SMIRNOV ...
            GOODNESS OF FIT Y
GENERALIZED LOGISTIC TYPE 3 CHI-SQUARE ...
            GOODNESS OF FIT Y


The following commands can be used to estimate the shape parameter for the generalized logistic type 3 distribution:

LET P1 = <value>
LET P2 = <value>
LET Q1 = <value>
LET Q2 = <value>
GENERALIZED LOGISTIC TYPE 4 PPCC PLOT Y
GENERALIZED LOGISTIC TYPE 4 KS PLOT Y


The default values for P1 and P2 are 0.1 and 10, respectively. The default values for Q1 and Q2 are 0.1 and 10, respectively.

Johnson, Kotz, and Balakrishnan (see Reference section below) also define type 1, type 3, type 4, and a parameterization due to Hoskings generalized logistic distributions. These are also supported by Dataplot (see the Related Commands section below).

None

None

GL4CDF	= Compute the generalized logistic type 4 cumulative distribution function.
GL4PPF	= Compute the generalized logistic type 4 percent point function.
GLOPDF	= Compute the generalized logistic type 1 probability density function.
GL2PDF	= Compute the generalized logistic type 2 probability density function.
GL3PDF	= Compute the generalized logistic type 3 probability density function.
GL5PDF	= Compute the generalized logistic (Hosking parameterization) probability density function.
LOGPDF	LOGPDF = Compute the logistic probability density function.
NORPDF	= Compute the normal probability density function.
LGNPDF	= Compute the logmormal probability density function.

"Continuous Univariate Distributions - 2", 2nd. Ed., Johnson, Kotz, and Balakrishnan, John Wiley, 1994 (pp. 140-147).

Data Analysis

2006/3

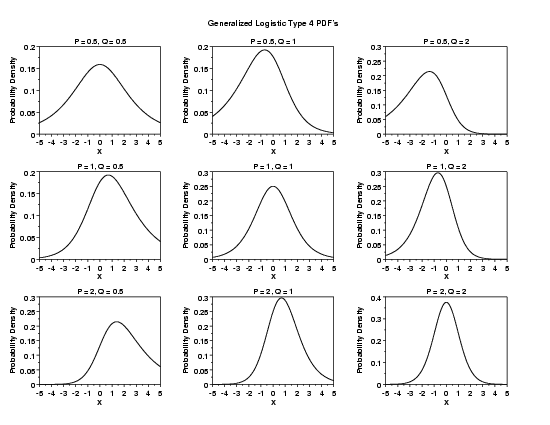
LET PA = DATA 0.5  1  2
LET QA = DATA 0.5  1  2
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
LABEL CASE ASIS
TITLE CASE ASIS
TITLE DISPLACEMENT 2
X1LABEL X
Y1LABEL Probability Density
X1LABEL DISPLACEMENT 14
Y1LABEL DISPLACEMENT 15
.
LOOP FOR K = 1 1 3
   LET P = PA(K)
   LOOP FOR L = 1 1 3
       LET Q = QA(L)
       TITLE P = ^P, Q = ^Q
       PLOT GL4PDF(X,P,Q) FOR X = -5  0.01  5
   END OF LOOP
END OF LOOP
END OF MULTIPLOT
CASE ASIS
MOVE 50 97
JUSTIFICATION CENTER
TEXT Generalized Logistic Type 4 PDF's