GTRPDF

GTRPDF (LET)

Library Function

Compute the generalized trapezoidal probability density function.

The regular trapezoidal distribution has the following probability density function:

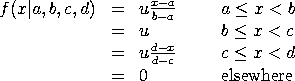
where

u = 2/(d + c - b - a) a <= b <= c <= d

Trapezoidal distributions may be appropriate for modeling processes that can be represented by the following three stages:

1. a growth stage
2. a period of relative stability stage
3. a decay stage

The trapezoidal model is probably the simplest model of this type (i.e., the growth and decline stages are linear and the stability stage is constant).

The generalized trapezoidal distribution allows more flexibility in modeling these stages. Specifically, the growth and decay stages may exhibit nonlinear convex or concave behavioir. In addition, the stability stage may be linearly increasing or decreasing.

The generalized trapezoid distribution has the following probability density function:

Dorp and Kotz (see Reference below) show that the generalized trapezoid can be defined as a mixture

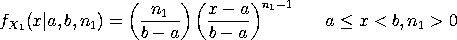
where the are positive and sum to 1 and where







and







This form may be more useful for modeling and fitting.

LET <y> = GTRPDF(<x>,<a>,<b>,<c> <d>,<nu1>,<nu3>,<alpha>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, number, or parameter containing values in the interval (a,d);
            <a> is a number, parameter, or variable that specifies the first shape parameter;
            <b> is a number, parameter, or variable that specifies the second shape parameter;
            <c> is a number, parameter, or variable that specifies the third shape parameter;
            <d> is a number, parameter, or variable that specifies the fourth shape parameter;
            <nu1> is a number, parameter, or variable that specifies the fifth shape parameter;
            <nu3> is a number, parameter, or variable that specifies the sixth shape parameter;
            <alpha> is a number, parameter, or variable that specifies the seventh shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = GTRPDF(0.65,0,0.2,0.8,1,2,2,0.5)
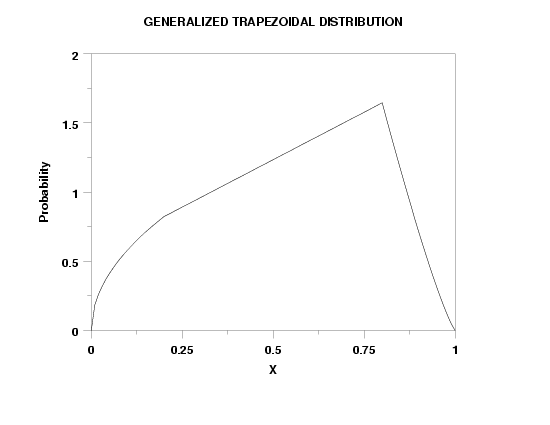
LET Y = GTRPDF(X,0,0.2,0.8,1,2,2,0.5)
LET Y = GTRPDF(X,A,B,C,D,NU1,NU3,ALPHA)

None

None

GTRPDF	= Compute the generalized trapezoidal cumulative distribution function.
GTRPPF	= Compute the generalized trapezoidal percent point function.
TRAPDF	= Compute the trapezoidal probability density function.
TRIPDF	= Compute the triangular probability density function.
UNIPDF	= Compute the uniform probability density function.
SEMPDF	= Compute the semi-circular probability density function.
NORPDF	= Compute the normal probability density function.

"Generalized Trapezoidal Distributions", van Dorp and Kotz, Metrika, Vol. 58, Issue 1, July, 2003.

Distributional Modeling

2004/1

 
TITLE GENERALIZED TRAPEZOIDAL DISTRIBUTION
LABEL CASE ASIS
X1LABEL X
Y1LABEL Probability
LET A = 0
LET B = 0.2
LET C = 0.8
LET D = 1
LET NU1 = 1.5
LET NU3 = 2.2
LET ALPHA = 0.5
PLOT GTRPDF(X,A,B,C,D,NU1,NU3,ALPHA) FOR X = A 0.01 D