SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

HERPPF

Name:
    HERPPF (LET)
Type:
    Library Function
Purpose:
    Compute the Hermite percent point function.
Description:
    If X1 and X2 are independent Poisson random variables with shape parameters alpha beta and (1/2)alpha2, respectively, then X1 + 2X2 follows a Hermite distribution with shape parameters alpha and beta.

    Some sources in the literature use the parameterization

      a = a1 = alpha beta
      b = a2 = 0.5alpha2

    The shape parameters alpha and beta can be expressed in terms of a1 and a2 as

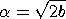
      alpha = SQRT(2*b)

      beta = a/SQRT(2*b)

    The probability mass function for the Hermite distribution is:

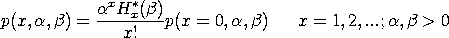
      p(x,alpha,beta) = (alpha**x*H*(x)(beta)/x!)*p(x=0,alpha,beta) x = 0, 1, 2, ...; alpha, beta > 0

      where

      p[x=0] = EXP[-alpha*beta - alpha**2/2]

    with H*(x)(beta) denoting the modified Hermite polynomial:

      H*(x)(beta) = SUM[j=0 to INT(N/2)][N!*X**(N-2*j)/((N-2(j)!j!2**j)]

    with [n/2] denoting the integer part of (n/2).

    The first few terms of the Hermite probability mass function are:

      p[x=0] = EXP[-alpha*beta - alpha**2/2]

      p[X=1] = alpha*beta*p[X=0]

      p[X=2] = (alpha**2*(beta**2+1)/2!)*p[X=0]

      p[X=3] = (alpha**3*(beta**3+3*beta)/3!)*p[X=0]

      p[X=4] = (alpha**4*(beta**4+6*beta**2+3)/4!)*p[X=0]

      p[X=5] = (alpha**5*(beta**5+10*beta**3+15*beta)/5!)*p[X=0]

    A general recuurence relation is:

      p[X=x+1] = (1/(x+1))*(alpha*beta*p[X=x] + alpha**2*p[X=x-1])

    Dataplot computes the Hermite percent point function by numerically inverting the Hermite cumulative distribution function. For x < 26, Dataplot uses the above recurrence relation to compute the probabilities. For x > 25, Dataplot uses an asymptotic formula due to Patel (see Reference section below) to compute the probabilities.

Syntax:
    LET <y> = HERPPF(<p>,<alpha>,<beta>)             <SUBSET/EXCEPT/FOR qualification>
    where <p> is a variable, number, or parameter in the range (0,1];
                <alpha> is a number or parameter that specifies the first shape parameter;
                <beta> is a number or parameter that specifies the second shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed Hermite ppf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = HERPPF(0.95,0.5,2)
    LET X2 = HERPPF(P,ALPHA,BETA)
    PLOT HERPPF(P,0.8,1.4) FOR P = 0 0.01 0.99
Default:
    None
Synonyms:
    None
Related Commands:
    HERCDF = Compute the Hermite cumulative distribution function.
    HERPDF = Compute the Hermite probability density function.
    POIPDF = Compute the Poisson cumulative distribution function.
    BINPDF = Compute the binomial probability density function.
    NBPDF = Compute the negative binomial probability density function.
    GEOPDF = Compute the geometric probability density function.
Reference:
    "Discrete Univariate Distributions" Second Edition, Johnson, and Kotz, and Kemp, Wiley, 1992, pp. 357-364.

    "An Asymptotic Expression for Cumulative Sum of Probabilities of the Hermite Distribution", Y. C. Patel, Communications in Statistics--Theory and Methods, 14, pp. 2233-2241.

Applications:
    Distributional Modeling
Implementation Date:
    2004/4
Program: 
     
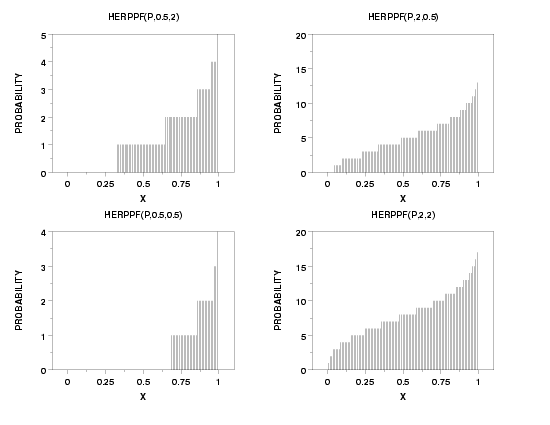
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
XTIC OFFSET 0.1 0.1
LINE BLANK
SPIKE ON
X1LABEL X
Y1LABEL PROBABILITY
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
TITLE SIZE 3
TITLE HERPPF(P,0.5,2)
PLOT HERPPF(P,0.5,2) FOR P = 0 0.01 0.99
TITLE HERPPF(P,2,0.5)
PLOT HERPPF(P,2,0.5) FOR P = 0 0.01 0.99
TITLE HERPPF(P,0.5,0.5)
PLOT HERPPF(P,0.5,0.5) FOR P = 0 0.01 0.99
TITLE HERPPF(P,2,2)
PLOT HERPPF(P,2,2) FOR P = 0 0.01 0.99
END OF MULTIPLOT
    plot generated by sample program

Date created: 7/7/2004
Last updated: 7/7/2004
Please email comments on this WWW page to alan.heckert@nist.gov.