IGAHAZ

IGAHAZ (LET)

Library Function

Compute the standard form of the inverted gamma hazard function.

The standard form of the inverted gamma hazard function is:
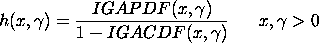
where is the shape parameter and IGAPDF and IGACDF are the probability density and cumulative distribution functions of the inverted gamma distribution.

The inverted gamma is a special case of the generalized gamma distribution where the second shape parameter is equal to -1.

LET <y> = IGAHAZ(<x>,<gamma>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a positive number, parameter, or a variable;
            <y> is a variable or a parameter (depending on what <x> is) where the computed inverted gamma hazard value is saved;
            <gamma> is a positive number, parameter, or variable that specifies the shape parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = IGAHAZ(3,1.5)
LET Y = IGAHAZ(X,1.5)
PLOT IGAHAZ(X,1.5) FOR X = 5 0.1 15

None

None

IGACDF	= Compute the inverted gamma cumulative distribution function.
IGAPDF	= Compute the inverted gamma probability density function.
IGAPPF	= Compute the inverted gamma percent point function.
GGDPDF	= Compute the generalized gamma probability density function.
GAMPDF	= Compute the gamma probability density function.
WEIPDF	= Compute the Weibull probability density function.
EXPPDF	= Compute the exponential probability density function.
CHSPDF	= Compute the chi-square probability density function.

"Continuous Univariate Distributions", 2nd. ed., Johnson, Kotz, and Balakrishnan, John Wiley and Sons, 1994 (chapter 17).

"Statistical Distributions", 2nd. Edition, Evans, Hastings, and Peacock, Wiley and Sons, 1993 (chapter 18).

Reliability

1998/5

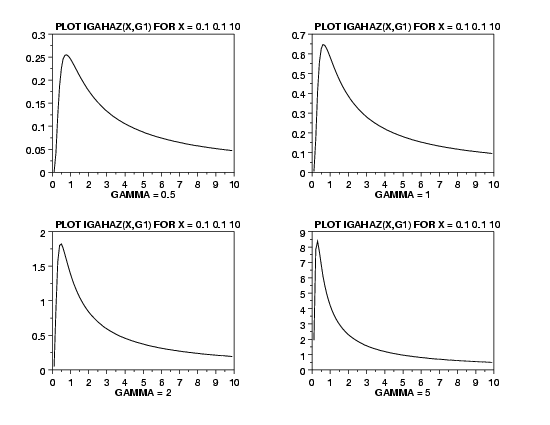
    LET G = DATA 0.5 1 2 5 
    . 
    MULTIPLOT 2 2 
    MULTIPLOT CORNER COORDINATES 0 0 100 100 
    TITLE AUTOMATIC 
    LOOP FOR K = 1 1 4 
       LET G1 = G(K) 
       X1LABEL GAMMA = ^G1 
       PLOT IGAHAZ(X,G1) FOR X = 0.1 0.1 10 
    END OF LOOP 
    END OF MULTIPLOT