IWECDF
Name:
Type:
Purpose:
Compute the standard form of the inverted Weibull cumulative
distribution function with tail length parameter
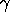 . .
Description:
The standard form of the inverted Weibull cumulative distribution
function is:
Syntax:
LET <y2> = IWECDF(<y1>,<GAMMA>)
<SUBSET/EXCEPT/FOR qualification>
where <y1> is a variable, number, or parameter;
<y2> is a variable or a parameter (depending on what
<y1> is) where the computed inverted Weibull cdf
value is stored;
<GAMMA> is a positive number or parameter that
specifies the tail length parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
LET A = IWECDF(3,2)
LET A = IWECDF(A1,4)
LET X2 = IWECDF(X1,8)
Note:
The general form of the inverted Weibull cumulative distribution
function is:
where 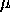 is the
location parameter and is the
location parameter and
 is the scale
parameter. is the scale
parameter.
Default:
Synonyms:
Related Commands:
|
IWEPDF
|
= Compute the inverted Weibull probability density
function.
|
|
IWEPPF
|
= Compute the inverted Weibull percent point function.
|
|
WEIPDF
|
= Compute the Weibull probability density function.
|
|
GAMPDF
|
= Compute the gamma probability density function.
|
|
CHSPDF
|
= Compute the chi-square probability density function.
|
|
NORPDF
|
= Compute the normal probability density function.
|
|
LOGPDF
|
= Compute the lognormal probability density function.
|
|
PPCC PLOT
|
= Generate a PPCC plot.
|
|
PROBABILTY PLOT
|
= Generate a probability plot.
|
|
RANDOM NUMBERS
|
= Generate random numbers.
|
Reference:
"Continuous Univariate Distributions: Volume 1", 2nd. Ed.,
Johnson, Kotz, and Balakrishnan, 1994, John Wiley, pp. 693.
Applications:
Implementation Date:
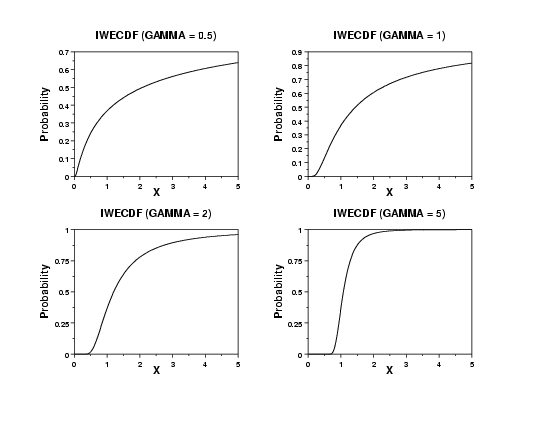
Program:
MULTIPOT 2 2
MULTIPLOT CORNER COORDINATES 5 5 95 95
MULTIPLOT SCALE FACTOR 2
LABEL CASE ASIS
Y1LABEL Probability
Y1LABEL DISPLACEMENT 12
X1LABEL X
TITLE IWECDF (GAMMA = 0.5)
PLOT IWECDF(X,0.5) FOR X = 0.01 0.01 5
TITLE IWECDF (GAMMA = 1)
PLOT IWECDF(X,1) FOR X = 0.01 0.01 5
TITLE IWECDF (GAMMA = 2)
PLOT IWECDF(X,2) FOR X = 0.01 0.01 5
TITLE IWECDF (GAMMA = 5)
PLOT IWECDF(X,5) FOR X = 0.01 0.01 5
END OF MULTIPLOT
Date created: 10/9/2001
Last updated: 4/4/2003
Please email comments on this WWW page to
alan.heckert@nist.gov.
|


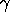 .
.
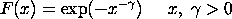
![F(x) =EXP{-[(x-u)/beta]**(-gamma)} x > mu; gamma, betas > 0](eqns/iwecdfg.gif)
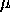 is the
location parameter and
is the
location parameter and
 is the scale
parameter.
is the scale
parameter.
